Refine listing
Actions for selected content:
149 results in 16Gxx
Linear free divisors and Frobenius manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 23 October 2009, pp. 1305-1350
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Poisson automorphisms and quiver moduli
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 653-667
- Print publication:
- July 2010
-
- Article
- Export citation
Cluster structures for 2-Calabi–Yau categories and unipotent groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 1035-1079
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Cluster complexes via semi-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 1001-1034
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
HOCHSCHILD (CO)HOMOLOGY OF ℤ2×ℤ2-GALOIS COVERINGS OF QUANTUM EXTERIOR ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 35-54
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Moduli spaces of orthogonal and symplectic bundles over an algebraic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 721-733
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Characterization of left Artinian algebras through pseudo path algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-416
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Counterexamples to Okounkov’s log-concavity conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1545-1557
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
The module structure of Solomon's descent algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-334
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
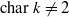 , and let Λ
, and let Λ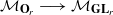 (respectively
(respectively 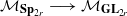 ) from the moduli space of orthogonal (respectively symplectic) bundles to the moduli space of all vector bundles over
) from the moduli space of orthogonal (respectively symplectic) bundles to the moduli space of all vector bundles over 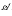 , ρ) with J
, ρ) with J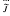
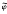 (Theorem 4.2),
(Theorem 4.2),