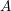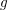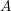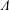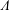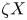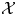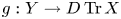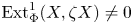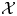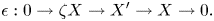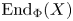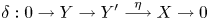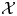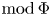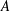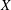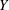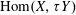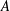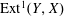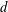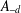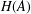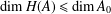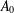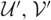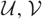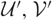Refine listing
Actions for selected content:
149 results in 16Gxx
COIDEMPOTENT SUBCOALGEBRAS AND SHORT EXACT SEQUENCES OF FINITARY 2-REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 19 March 2020, pp. 316-341
- Print publication:
- September 2021
-
- Article
- Export citation
Tropical friezes and the index in higher homological algebra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 23-49
- Print publication:
- July 2021
-
- Article
- Export citation
LOCAL DUALITY FOR THE SINGULARITY CATEGORY OF A FINITE DIMENSIONAL GORENSTEIN ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 1-24
- Print publication:
- December 2021
-
- Article
- Export citation
MIXED HODGE STRUCTURES WITH MODULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 02 March 2020, pp. 161-195
- Print publication:
- January 2022
-
- Article
- Export citation
Counting Higgs bundles and type
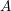 $A$ quiver bundles
$A$ quiver bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 27 February 2020, pp. 744-769
- Print publication:
- April 2020
-
- Article
- Export citation
Coxeter Diagrams and the Köthe’s Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 656-686
- Print publication:
- June 2021
-
- Article
- Export citation
On Extensions for Gentle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 249-292
- Print publication:
- February 2021
-
- Article
- Export citation
d-Auslander–Reiten sequences in subcategories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 15 January 2020, pp. 342-373
-
- Article
- Export citation
Rigidity dimension of algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 26 November 2019, pp. 417-443
- Print publication:
- March 2021
-
- Article
- Export citation
TAME BLOCK ALGEBRAS OF HECKE ALGEBRAS OF CLASSICAL TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 September 2019, pp. 179-201
- Print publication:
- October 2021
-
- Article
- Export citation
Balanced pairs, cotorsion triplets and quiver representations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 13 August 2019, pp. 67-90
-
- Article
- Export citation
On the Combinatorics of Gentle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 1551-1580
- Print publication:
- December 2020
-
- Article
- Export citation
ON GRADED SYMMETRIC CELLULAR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 349-362
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
LOCALIZATIONS OF THE HEARTS OF COTORSION PAIRS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 564-583
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
CLUSTER CATEGORIES FROM GRASSMANNIANS AND ROOT COMBINATORICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 03 June 2019, pp. 322-354
- Print publication:
- December 2020
-
- Article
- Export citation
n-T-COTORSION-FREE MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 297-311
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
ALGEBRAS OF GENERALIZED DIHEDRAL TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 181-236
- Print publication:
- December 2020
-
- Article
- Export citation
ORIENTED FLIP GRAPHS, NONCROSSING TREE PARTITIONS, AND REPRESENTATION THEORY OF TILING ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 147-182
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Local duality for representations of finite group schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 424-453
- Print publication:
- February 2019
-
- Article
-
- You have access
- HTML
- Export citation
Approximations, ghosts and derived equivalences
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 813-840
- Print publication:
- April 2020
-
- Article
- Export citation