Refine listing
Actions for selected content:
322 results in 05-XX
A natural representation of partitions as terms of a universal algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-324
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
On some first-crossing-time probabilities for a two-dimensional random walk with correlated components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 441-454
- Print publication:
- June 1992
-
- Article
- Export citation
Asymptotic reliability of consecutive k-out-of-n systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-155
- Print publication:
- March 1992
-
- Article
- Export citation
Is the Union-closed sets conjecture the best possible?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 276-283
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
On the average number of real zeros of a class of random algebraic equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-160
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Bijective Proofs of Some n-Color Partition Identities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-332
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
Une Note sur les Coefficients Binomiaux de Gauss
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-343
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
A generalisation of the quintuple product identity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 42-45
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
Basic representations of some affine Lie algebras and generalized Euler identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 296-311
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Lower bound for the number of real roots of a random algebraic polynomial
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-27
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
On Kruskal's cascades and counting containments in a set of subsets
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-141
- Print publication:
- June 1983
-
- Article
- Export citation
A generalization of Sperner's theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-485
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
On ordered set systems and some conjectures related to the erdös–ko–rado theorem and turán's theorem
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-66
- Print publication:
- June 1981
-
- Article
- Export citation
Some asymptotic methods in combinatorics
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 452-460
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Four-discordant permutations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-377
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation
Retracts of partially ordered sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 4 / June 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 495-506
- Print publication:
- June 1979
-
- Article
-
- You have access
- Export citation
Some intersection and union theorems for several families of finite sets
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-128
- Print publication:
- June 1978
-
- Article
- Export citation
An asymptotic expansion for the Wedderburn–Etherington sequence
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 262-265
- Print publication:
- December 1977
-
- Article
- Export citation
On a problem of P. Erdős
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 226-228
- Print publication:
- December 1973
-
- Article
- Export citation
On incomparable collections of sets
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 208-209
- Print publication:
- December 1973
-
- Article
- Export citation
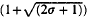 log
log 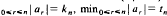 and ε
and ε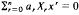 then for
then for 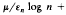
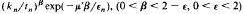 provided lim
provided lim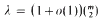 ,
, 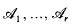
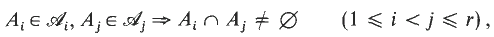
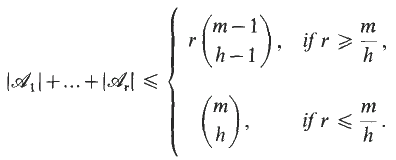
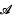 is a collection of distinct subsets of {1, …,
is a collection of distinct subsets of {1, …, 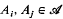 ,
, 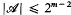 .
.