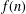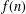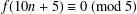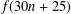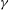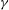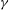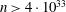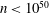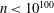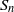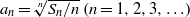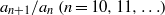Refine listing
Actions for selected content:
330 results in 05-XX
DUAL EQUIVALENCE GRAPHS I: A NEW PARADIGM FOR SCHUR POSITIVITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 22 July 2015, e12
-
- Article
-
- You have access
- Open access
- Export citation
ARITHMETIC PROPERTIES OF PARTITION QUADRUPLES WITH ODD PARTS DISTINCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 353-364
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A Combinatorial Approach to a Model of Constrained Random Walkers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 16 March 2015, pp. 222-235
-
- Article
- Export citation
Partial Shadows of Set Systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 20 January 2015, pp. 825-828
-
- Article
- Export citation
Minimum Number of Monotone Subsequences of Length 4 in Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 19 December 2014, pp. 658-679
-
- Article
- Export citation
A NEW CONGRUENCE MODULO 25 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 41-46
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
CANONICAL REPRESENTATIVES FOR DIVISOR CLASSES ON TROPICAL CURVES AND THE MATRIX–TREE THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 26 September 2014, e24
-
- Article
-
- You have access
- Open access
- Export citation
INFINITE FAMILIES OF CONGRUENCES MODULO 3 AND 9 FOR BIPARTITIONS WITH 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 August 2014, pp. 47-52
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
GENERALISATION OF KEITH’S CONJECTURE ON 9-REGULAR PARTITIONS AND 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 204-212
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON
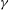 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma $-VECTORS AND THE DERIVATIVES OF THE TANGENT AND SECANT FUNCTIONS
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma $-VECTORS AND THE DERIVATIVES OF THE TANGENT AND SECANT FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 177-185
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
COUNTING SYMMETRIC COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1-8
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
On Generalized Pólya Urn Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1169-1186
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 473-478
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
COUNTING SYMMETRIC BRACELETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 431-436
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO POWERS OF 2 FOR FU’S 5 DOTS BRACELET PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 360-372
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
SYSTEMS OF ISLANDS WITH CONTINUOUS HEIGHT FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 385-396
-
- Article
-
- You have access
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
NOTE ON ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 448-451
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA: COMPUTATION AND REAL EHRHART THEORY
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 05 September 2012, pp. 1-22
- Print publication:
- January 2013
-
- Article
- Export citation