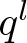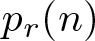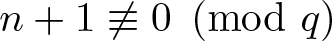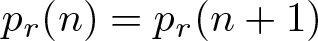Refine listing
Actions for selected content:
330 results in 05-XX
GALOIS GROUPS OF APÉRY-LIKE SERIES MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 February 2026, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graphical sequences and plane trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 05 February 2026, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lorentzian polynomials on cones
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 26 January 2026, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINATORIAL PROOFS OF CERTAIN RESULTS OF CHEN AND ZOU ON TWO-COLOUR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-7
-
- Article
- Export citation
Enriched cycle structures and roots of permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 January 2026, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
Overpartitions with parts separated by parity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The finite forms of MacMahon’s q-series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 January 2026, pp. 1-28
-
- Article
- Export citation
Toric arc schemes and q-enumeration of lattice points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free fermionic probability theory and k-theoretic schubert calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit formulas for the Grothendieck class of
 $\overline {\mathcal{M}}_{0,n}$
$\overline {\mathcal{M}}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequalities for the sequences with unified form
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-20
-
- Article
- Export citation
Self-avoiding walk is ballistic on graphs with more than one end
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 October 2025, e179
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequality arising from the iterated Laguerre operator for various partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-22
-
- Article
- Export citation
Some algebraic properties of ASM varieties
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 October 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF PARTS IN A RANDOM t-REGULAR PARTITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 2 / February 2026
- Published online by Cambridge University Press:
- 13 October 2025, pp. 543-574
- Print publication:
- February 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Alternating sign matrices with reflective symmetry and plane partitions:
 $n+3$ pairs of equivalent statistics and a Cauchy-type identity
$n+3$ pairs of equivalent statistics and a Cauchy-type identity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e168
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the f-vectors of flow polytopes for the complete graph
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic structure of Dyson–Schwinger equations with multiple insertion places
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2026
- Published online by Cambridge University Press:
- 29 August 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modified ascent sequences avoiding a pattern of length 4
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1390-1418
-
- Article
- Export citation