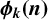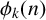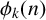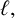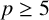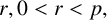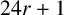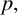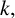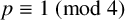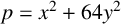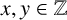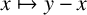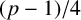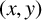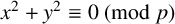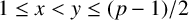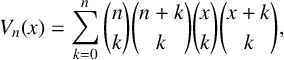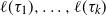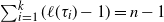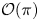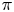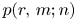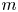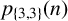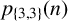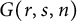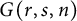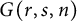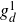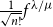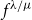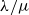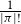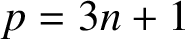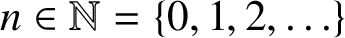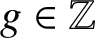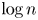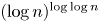Refine listing
Actions for selected content:
322 results in 05-XX
ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS
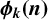 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 431-436
- Print publication:
- December 2022
-
- Article
- Export citation
ALTERNATING CIRCULAR SUMS OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 385-395
- Print publication:
- December 2022
-
- Article
- Export citation
A NEW CHARACTERISATION FOR QUARTIC RESIDUACITY OF
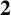 $\mathbf {2}$
$\mathbf {2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1-6
- Print publication:
- August 2022
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS INVOLVING APÉRY-LIKE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 203-208
- Print publication:
- October 2022
-
- Article
- Export citation
Random stable-type minimal factorizations of the n-cycle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 24 February 2022, pp. 1-63
- Print publication:
- March 2022
-
- Article
- Export citation
Some generating functions and inequalities for the andrews–stanley partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 120-135
-
- Article
- Export citation
Tuning as convex optimisation: a polynomial tuner for multi-parametric combinatorial samplers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 765-811
-
- Article
- Export citation
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
- Print publication:
- August 2022
-
- Article
- Export citation
Polynomiality of factorizations in reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 245-266
- Print publication:
- February 2023
-
- Article
- Export citation
Tevelev degrees and Hurwitz moduli spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 479-510
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arcsine laws for random walks generated from random permutations with applications to genomics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 851-867
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
Lower bound on the size of a quasirandom forcing set of permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 27 July 2021, pp. 304-319
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetry of Narayana Numbers and Rowvacuation of Root Posets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CUBES IN FINITE FIELDS AND RELATED PERMUTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 15 July 2021, pp. 188-196
- Print publication:
- April 2022
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 415-423
- Print publication:
- December 2021
-
- Article
- Export citation
Most permutations power to a cycle of small prime length
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 24 May 2021, pp. 234-246
-
- Article
- Export citation
ENUMERATING NECKLACES WITH TRANSITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 1-11
- Print publication:
- February 2022
-
- Article
- Export citation
Log-concavity and log-convexity of moments of averages of i.i.d. random variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 271-278
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting matchings via capacity-preserving operators
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation