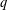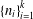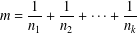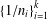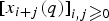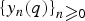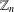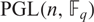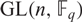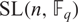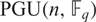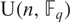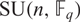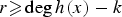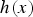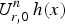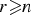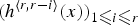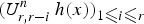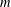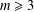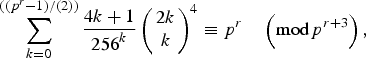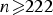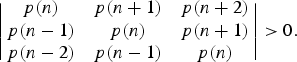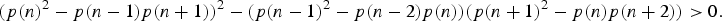Refine listing
Actions for selected content:
318 results in 05-XX
On the rate of convergence for the length of the longest common subsequences in hidden Markov models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 558-573
- Print publication:
- June 2019
-
- Article
- Export citation
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 May 2019, e17
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON THE SUM OF RECIPROCALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 189-193
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
The Shifted Turán Sieve Method on Tournaments
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 April 2019, pp. 841-855
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 41-47
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Positivity and continued fractions from the binomial transformation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 18 March 2019, pp. 831-847
- Print publication:
- June 2019
-
- Article
- Export citation
An Elementary Proof of Bevan's Theorem on the Growth of Grid Classes of Permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 975-984
-
- Article
- Export citation
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE RANK STATISTIC FOR STRONGLY CONCAVE COMPOSITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 230-238
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Limit laws of planar maps with prescribed vertex degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 04 February 2019, pp. 519-541
-
- Article
- Export citation
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 93-107
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Interlacing polynomials and the veronese construction for rational formal power series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1-16
- Print publication:
- February 2020
-
- Article
- Export citation
INTEGER POLYGONS OF GIVEN PERIMETER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 131-147
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Some congruences involving fourth powers of central q-binomial coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1127-1138
- Print publication:
- June 2020
-
- Article
- Export citation
Determinantal inequalities for the partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1451-1466
- Print publication:
- June 2020
-
- Article
- Export citation
Boardman–Vogt tensor products of absolutely free operads
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 367-385
- Print publication:
- February 2020
-
- Article
- Export citation
Infinite families of congruences modulo 5 and 7 for the cubic partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1189-1205
- Print publication:
- October 2019
-
- Article
- Export citation
A Boltzmann Approach to Percolation on Random Triangulations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1-43
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
- Print publication:
- 2019
-
- Article
- Export citation
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 929-949
- Print publication:
- 2019
-
- Article
- Export citation