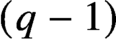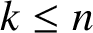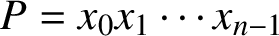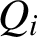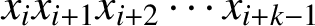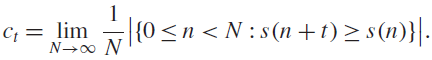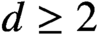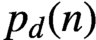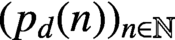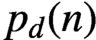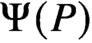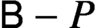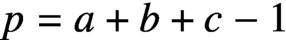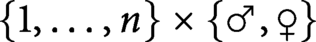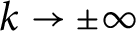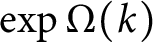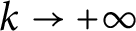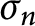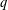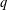Refine listing
Actions for selected content:
322 results in 05-XX
A Symmetric Function of Increasing Forests
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 April 2021, e35
-
- Article
-
- You have access
- Open access
- Export citation
ASKING QUESTIONS TO DETERMINE THE PRODUCT OF CIRCULARLY ARRANGED NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 April 2021, pp. 187-195
- Print publication:
- October 2021
-
- Article
- Export citation
A NEW REFINEMENT OF FINE’S PARTITION THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 353-361
- Print publication:
- December 2021
-
- Article
- Export citation
On a generalization of the Rényi–Srivastava characterization of the Poisson law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 68-82
- Print publication:
- March 2021
-
- Article
- Export citation
A lower bound for Cusick’s conjecture on the digits of n + t
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 139-161
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
The number of maximum primitive sets of integers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 781-795
-
- Article
- Export citation
SOME OBSERVATIONS AND SPECULATIONS ON PARTITIONS INTO d-TH POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 406-414
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
BIASES IN INTEGER PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 177-186
- Print publication:
- October 2021
-
- Article
- Export citation
DIVISIBILITY OF CERTAIN SINGULAR OVERPARTITIONS BY POWERS OF
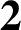 $\textbf{2}$ AND
$\textbf{2}$ AND 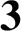 $\textbf{3}$
$\textbf{3}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 238-248
- Print publication:
- October 2021
-
- Article
- Export citation
ON THE SUM OF PARTS IN THE PARTITIONS OF n INTO DISTINCT PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 December 2020, pp. 228-237
- Print publication:
- October 2021
-
- Article
- Export citation
Dynamics of plane partitions: Proof of the Cameron–Fon-Der-Flaass conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 07 December 2020, 62
-
- Article
-
- You have access
- Open access
- Export citation
MULTINOMIAL VANDERMONDE CONVOLUTION VIA PERMANENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 353-361
- Print publication:
- June 2021
-
- Article
- Export citation
Subgraph counts for dense random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 460-497
-
- Article
- Export citation
Asymptotic normality in t-stack sortable permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 November 2020, pp. 1062-1070
-
- Article
- Export citation
Newman's identities, lucas sequences and congruences for certain partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 October 2020, pp. 709-736
-
- Article
- Export citation
Beyond Beatty sequences: Complementary lattices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 06 August 2020, pp. 499-511
- Print publication:
- September 2021
-
- Article
- Export citation
Mallows permutations as stable matchings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 27 July 2020, pp. 1531-1555
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
Graph limits of random unlabelled k-trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 18 May 2020, pp. 722-746
-
- Article
-
- You have access
- Open access
- Export citation
SUMS OF PARTIAL THETA FUNCTIONS THROUGH AN EXTENDED BAILEY TRANSFORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 May 2020, pp. 1-10
- Print publication:
- February 2021
-
- Article
- Export citation
A TRUNCATED IDENTITY OF EULER AND RELATED
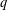 $q$-CONGRUENCES
$q$-CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2020, pp. 353-359
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation