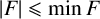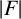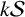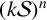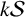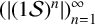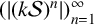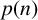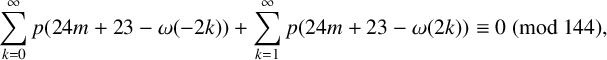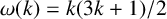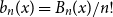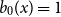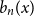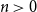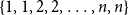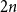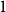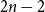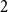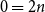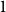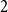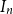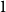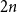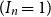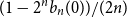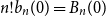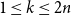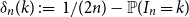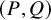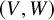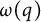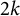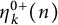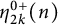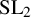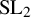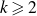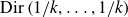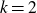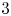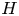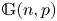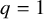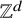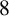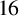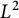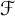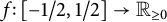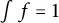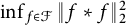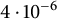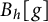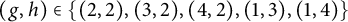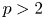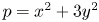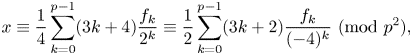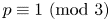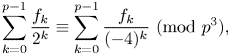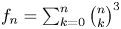Refine listing
Actions for selected content:
322 results in 05-XX
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 535-562
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp large deviations and concentration inequalities for the number of descents in a random permutation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 810-833
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING UNIONS OF SCHREIER SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 19-31
- Print publication:
- August 2024
-
- Article
- Export citation
DIVISIBILITY OF SUMS OF PARTITION NUMBERS BY MULTIPLES OF 2 AND 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 271-279
- Print publication:
- October 2024
-
- Article
- Export citation
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 30 November 2023, pp. 954-974
- Print publication:
- June 2025
-
- Article
- Export citation
The Bernoulli clock: probabilistic and combinatorial interpretations of the Bernoulli polynomials by circular convolution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 210-237
-
- Article
- Export citation
Burstein’s permutation conjecture, Hong and Li’s inversion sequence conjecture and restricted Eulerian distributions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1179-1201
-
- Article
- Export citation
Skew RSK dynamics: Greene invariants, affine crystals and applications to q-Whittaker polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 October 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics for symmetrized positive moments of odd ranks
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1731-1752
- Print publication:
- October 2024
-
- Article
- Export citation
A combinatorial model for the transition matrix between the Specht and
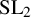 $\operatorname {SL}_2$-web bases
$\operatorname {SL}_2$-web bases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 September 2023, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation
Subgraph distributions in dense random regular graphs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 August 2023, pp. 2125-2148
- Print publication:
- October 2023
-
- Article
- Export citation
New mock theta functions and formulas for basic hypergeometric series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 868-896
-
- Article
- Export citation
Remixed Eulerian numbers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 July 2023, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MacMahon’s statistics on higher-dimensional partitions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A CONJECTURE FOR A REFINEMENT OF THE SUM OF MINIMAL EXCLUDANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 July 2023, pp. 276-287
- Print publication:
- April 2024
-
- Article
- Export citation
Floor diagrams and enumerative invariants of line bundles over an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. 1741-1790
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An optimal
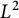 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 108-121
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 215-224
- Print publication:
- April 2024
-
- Article
- Export citation