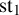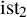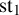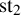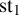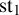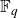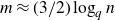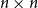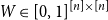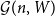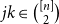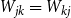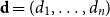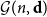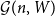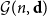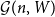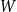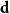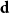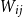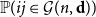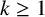Refine listing
Actions for selected content:
322 results in 05-XX
A REMARK ON GENERALISED CUBIC PARTITIONS MODULO
 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 May 2025, pp. 1-5
-
- Article
- Export citation
ON
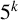 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 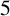 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 449-457
- Print publication:
- December 2025
-
- Article
- Export citation
COMBINATORIAL PROOFS FOR TWO-COLOUR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-5
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NEW TRUNCATED IDENTITIES AND PARTITION THEOREMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-8
-
- Article
- Export citation
ON NEW MINIMAL EXCLUDANTS OF OVERPARTITIONS RELATED TO SOME q-SERIES OF RAMANUJAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-13
- Print publication:
- August 2025
-
- Article
- Export citation
Pebble trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DERIVATIVES OF THETA FUNCTIONS AS TRACES OF PARTITION EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 284-295
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BASE SHIFTING SEQUENCES AND THE PALINDROME PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 385-396
- Print publication:
- June 2025
-
- Article
- Export citation
Asymptotics for crank of overpartitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-34
-
- Article
- Export citation
On the binomial transforms of Apéry-like sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 359-376
- Print publication:
- June 2025
-
- Article
- Export citation
The dimension of the feasible region of pattern densities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-14
- Print publication:
- January 2025
-
- Article
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING CONGRUENCES FOR OVERPARTITIONS WITH
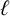 $\ell $-REGULAR NONOVERLINED PARTS
$\ell $-REGULAR NONOVERLINED PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 478-489
- Print publication:
- June 2025
-
- Article
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
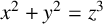 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation
Equality cases of the Alexandrov–Fenchel inequality are not in the polynomial hierarchy
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-sided permutation statistics via symmetric functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth permutations and polynomials revisited
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 11 December 2024, pp. 455-480
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding theorems for random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 16 October 2024, pp. 115-130
-
- Article
- Export citation
ON A CONJECTURE REGARDING THE SYMMETRIC DIFFERENCE OF CERTAIN SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 397-404
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation











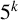
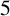



















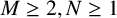

















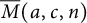



















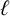
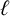
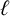
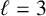
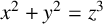





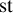
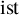
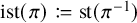 . We give a general approach, based on the theory of symmetric functions, for finding the joint distribution of
. We give a general approach, based on the theory of symmetric functions, for finding the joint distribution of