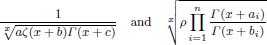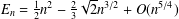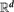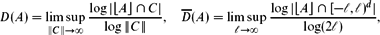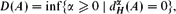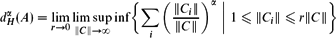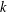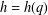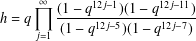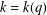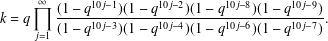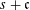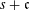Refine listing
Actions for selected content:
318 results in 05-XX
On a random search tree: asymptotic enumeration of vertices by distance from leaves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 850-876
- Print publication:
- September 2017
-
- Article
- Export citation
Log-concavity and strong q-log-convexity for Riordan arrays and recursive matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1297-1310
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
TWO NEW LOWER BOUNDS FOR THE SPARK OF A MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 353-360
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Critical Window for Connectivity in the Configuration Model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 29 May 2017, pp. 660-680
-
- Article
- Export citation
From coin tossing to rock-paper-scissors and beyond: a log-exp gap theorem for selecting a leader
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 213-235
- Print publication:
- March 2017
-
- Article
- Export citation
CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 157-176
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF
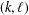 $(k,\ell )$ -REGULAR BIPARTITIONS
$(k,\ell )$ -REGULAR BIPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 353-364
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
The Monotonicity and Log-Behaviour of Some Functions Related to the Euler Gamma Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 November 2016, pp. 527-543
-
- Article
- Export citation
THE DIMENSION OF CENTRALISERS OF MATRICES OF ORDER
 $n$
$n$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 353-361
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
A Determinant Identity Implying the Lagrange–Good Inversion Formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 165-176
-
- Article
- Export citation
ENUMERATION OF A DUAL SET OF STIRLING PERMUTATIONS BY THEIR ALTERNATING RUNS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 177-186
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Multivariate Eulerian Polynomials and Exclusion Processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 18 March 2016, pp. 486-499
-
- Article
- Export citation
Marstrand-type Theorems for the Counting and Mass Dimensions in ℤ
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 700-743
-
- Article
- Export citation
Application of Braiding Sequences. II. Polynomial Invariants of Positive Knots
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 1037-1064
-
- Article
- Export citation
Computing cup products in integral cohomology ofHilbert schemes of points on K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 78-97
-
- Article
-
- You have access
- Export citation
Probabilistic Divide-and-Conquer: A New Exact Simulation Method, With Integer Partitions as an Example
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 324-351
-
- Article
- Export citation
THE LEVEL 12 ANALOGUE OF RAMANUJAN’S FUNCTION
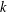 $k$
$k$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
The Inversion Number and the Major Index are Asymptotically Jointly Normally Distributed on Words
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 14 January 2016, pp. 470-483
-
- Article
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA II: BIDEGREE AND POISSON FORMULA
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 653-684
- Print publication:
- 2016
-
- Article
- Export citation
A NOTE ON RANDOM MATRIX INTEGRALS, MOMENT IDENTITIES, AND CATALAN NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 811-817
- Print publication:
- 2016
-
- Article
- Export citation
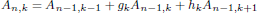
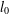
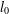
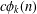
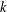

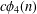
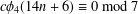
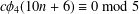
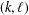
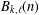
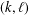

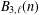
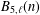
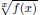 is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions
is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions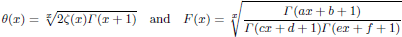
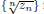 for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients
for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients 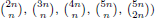 are demonstrated. In particular, this contains some results of Chen
are demonstrated. In particular, this contains some results of Chen 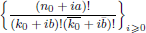
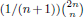 and the central binomial coefficients
and the central binomial coefficients 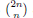 are infinitely log-monotonic, and strengthens one result of Su and Wang that
are infinitely log-monotonic, and strengthens one result of Su and Wang that 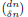 is log-convex in
is log-convex in