Refine listing
Actions for selected content:
318 results in 05-XX
The asymptotic joint normality of the numbers of upper records, lower records and inversions in a random sequence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 257-263
- Print publication:
- March 2003
-
- Article
- Export citation
Multipartitions, generalized Durfee squares and affine Lie algebra characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 01 August 2017, pp. 395-408
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Combinatorial techniques for M/G/1-type queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 722-736
- Print publication:
- September 2001
-
- Article
- Export citation
Addendum to ‘Quasi-renewal estimates’ for modelling DNA replication
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1171-1172
- Print publication:
- December 2000
-
- Article
- Export citation
The formal theory of birth-and-death processes, lattice path combinatorics and continued fractions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 750-778
- Print publication:
- September 2000
-
- Article
- Export citation
Asymptotics of pooling design performance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 951-964
- Print publication:
- December 1999
-
- Article
- Export citation
Epidemic processes on digraphs of random mappings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 780-798
- Print publication:
- September 1999
-
- Article
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation
Pascal's triangles in Abelian and hyperbolic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-288
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
A new proof of the Macdonald identities for An−1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-360
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Renewal-type behavior of absorption times in Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 988-1005
- Print publication:
- December 1994
-
- Article
- Export citation
A note on the union-closed sets conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-236
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
How to obtain an asymptotic expansion of a sequence from an analytic identity satisfied by its generating function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-143
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Transient analysis of M/M/1 queues in discrete time by general server vacations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-129
- Print publication:
- 1994
-
- Article
- Export citation
A note of the union-closed sets conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-413
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
Decomposition of sets of small or large boundary
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 290-304
- Print publication:
- December 1993
-
- Article
- Export citation
A natural representation of partitions as terms of a universal algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-324
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
On some first-crossing-time probabilities for a two-dimensional random walk with correlated components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 441-454
- Print publication:
- June 1992
-
- Article
- Export citation
Asymptotic reliability of consecutive k-out-of-n systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-155
- Print publication:
- March 1992
-
- Article
- Export citation
Is the Union-closed sets conjecture the best possible?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 276-283
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
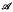 there exists some element which is contained in at least half the sets in
there exists some element which is contained in at least half the sets in 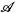 = {A
= {A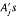 .
.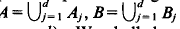 and vectors
and vectors 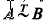 In [3], Theorem 3 we proved that if
In [3], Theorem 3 we proved that if