This paper gives variants of results from classical algebraic geometry and commutative algebra for quadratic algebras with conjugation. Quadratic algebras are essentially two-dimensional algebras with identity over commutative rings with identity, on which a natural operation of conjugation may be defined. We define the ring of conjugate polynomials over a quadratic algebra, and define c-varieties. In certain cases a close correspondence between standard varieties and c-varieties is demonstrated, and we establish a correspondence between conjugate and standard polynomials, which leads to variants of the Hilbert Nullstellensatz if the commutativering is an algebraically closed field. These results may be applied to automated Euclidean geometry theorem proving.

An extension R1 of a right chain ring R is called immediate if R1 has the same residue division ring and the same lattice of principal right ideals as R. Properties of such immediate extensions are studied. It is proved that for every R, maximal immediate extensions exist, but that in contrast to the commutative case maximal right chain rings are not necessarily linearly compact.

For any ring S we define and describe its characteristic ring, k(S). It plays the rôle of the usual characteristic even in rings whose additive structure, (S, +), is complicated. The ring k(S) is an invariant of (S, +) and also reflects certain non-additive properties of S. If R is a left faithful ring without identity element, we show how to use k(R) to embed R in a ring R1 with identity. This unital overring of R inherits many ring properties of R; for instance, if R is artinian, noetherian, semiprime Goldie, regular, biregular or a V-ring, so too is R1. In the case of regularity (or generalizations thereof), R1 satisfies a universal property with respect to the adjunction of an identity

Differentially simple local noetherian Q -algebras are shown to be always (a certain type of) subrings of formal power series rings. The result is established as an illustration of a general theory of differential filtrations and differential completions.

Filters and אּ-complete filters can be used to produce set-theoretic extensions of direct sums and direct products. They can be applied to generalize theorems in module theory which involve these. For example, the theorem, stating that a ring is noetherian, if, and only if, direct sums of injectives are injective, can be generalized, provided we replace noetherian by Xa-noetherian and direct sums by אּ- complete filter sums with a suitable property.

It is well known that for a ring with identity the Brown-McCoy radical is the maximal small ideal. However, in certain subrings of complete matrix rings, which we call structural matrix rings, the maximal small and minimal essential ideals coincide.

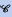In this paper we characterize a class of commutative and a class of non-commutative rings for which this coincidence occurs, namely quotients of Prüfer domains and structural matrix rings over Brown-McCoy semisimple rings. A similarity between these two classes is obtained.

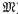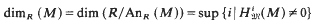
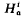Let (R, ) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated R-module M to have a system of parameters. We prove that if

then any system of parameters for R/AnR (M) is a system of parameters for M. As an application we characterize by means of systems of parameters those balanced big Cohen–Macaulay R-modules M for which SuppR (M) = suppR (M).

The concept of a permutation polynomial function over a commutative ring with 1 can be generalized to multiplace functions in two different ways, yielding the notion of a k-ary permutation polynomial function (k > 1, k ∈ N) and the notion of a strict k-ary permutation polynomial function respectively. It is shown that in the case of a residue class ring Zm of the integers these two notions coincide if and only if m is squarefree.

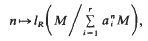
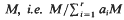Throughout this paper A is a commutative noetherian ring (with identity) and M is an A-module. We use to denote, for i ≥ 0, the i-th right derived functor of the local cohomology functor L with respect to an ideal a of A [8; 2.1].

Throughout this note the letters D and K denote a commutative integral domain with 1 and its field of fractions.

It is well-known that if R is a commutative ring with identity, M is a Noetherian R-module and I is an ideal of R such that M/IM has finite length, then the function n → lR (M /InM) is a polynomial function for n large (cf. [3], p. II-25), where lR denotes length as an R-module. In this note we are concerned with the function

where a1, … , ar is a multiplicity system for has finite length.

Let R be an associative ring which is not necessarily commutative. For any torsion theory τ on the category of left R-modules and for any nonnegative integer n we define and study the notion of the nth local cohomology functor with respect to τ. For suitably nice rings a bound for the nonvanishing of these functors is given in terms of the τ-dimension of the modules.

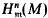The purpose of this paper is to provide additional evidence to support our view that the modules of generalized fractions introduced in [8] are worth further investigation: we show that, for a module M over a (commutative, Noetherian) local ring A (with identity) having maximal ideal m and dimension n, the n-th local cohomology module may be viewed as a module of generalized fractions of M with respect to a certain triangular subset of An + 1, and we use this work to formulate Hochster's ‘Monomial Conjecture’ [2, Conjecture 1]; in terms of modules of generalized fractions and to make a quick deduction of one of Hochster's results which supports that conjecture.

A Boolean-like ring R is a commutative ring with unity in which 2x = 0 and xy(1 + x)(1 + y) = 0 hold for all elements x, y of the ring R. It is shown in this paper that in the category of Boolean-like rings, R is injective if and only if R is a complete Boolean ring and R is projective if and only if R = {0, 1}.

The construction, for a module M over a commutative ring A (with identity) and a multiplicatively closed subset S of A, of the module of fractions S-1M is, of course, one of the most basic ideas in commutative algebra. The purpose of this note is to present a generalization which constructs, for a positive integer n and what is called a triangular subset U of An = A × A × … × A (n factors), a module U-n M of generalized fractions, a typical element of which has the form

where m∈ M and (u1, … un)∈U.

A module M over a ring R is κ-projective, κ a cardinal, if M is projective relative to all exact sequence of R-modules 0 → A → B → C → 0 such that C has a generating set of cardinality less than κ. A structure theorem for κ-projective modules over Dedekind domains is proven, and the κ-projectivity of M is related to properties of ExtR (M, ⊕ R). Using results of S. Chase, S. Shelah and P. Eklof, the existence of non-projective и1-projective modules is shown to undecidable, while both the Continuum Hypothesis and its denial (Plus Martin's Axiom) imply the existence of a reduced И0-projective Z-module which is not free.

Let R be a commutative ring with identity, and let A be a finitely generated R-algebra with Jacobson radical N and center C. An R-inertial subalgebra of A is a R-separable subalgebra B with the property that B+N=A. Suppose A is separable over C and possesses a finite group G of R-automorphisms whose restriction to C is faithful with fixed ring R. If R is an inertial subalgebra of C, necessary and sufficient conditions for the existence of an R-inertial subalgebra of A are found when the order of G is a unit in R. Under these conditions, an R-inertial subalgebra B of A is characterized as being the fixed subring of a group of R-automorphisms of A. Moreover, A ⋍ B ⊗R C. Analogous results are obtained when C has an R-inertial subalgebra S ⊃ R.

Let N be a direct summand of a module which is a direct sum of modules of torsion-free rank one over a discrete valuation ring. Then there is a torsion module T such that N⊕T is also a direct sum of modules of torsion-free rank one.

Let L/K be a quadratic extension of algebraic number fields, and D a central L-division algebra of finite L-dimension d2. If - is an involution (i.e., a ring antiautomorphism of period two) of D, we write S(-) for the set of - symmetric elements of D:

Let R be a commutative ring with identity, and let U be a unitary commutative R-algebra with identity. In [1] Gilmer defines the (l/n)th power (n a positive integer) of a valuation ideal R when R is a domain. Sections 2, 3 of the present note are devoted to the study of an extension of this notion to positive rational powers of an arbitrary R-submodule of U.