Refine listing
Actions for selected content:
447 results in 13xxx
ℤ[1/p]-motivic resolution of singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1434-1446
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
COFINITENESS OF GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 29 March 2011, pp. 382-388
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Green’s conjecture for curves on arbitrary K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 839-851
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
On two examples by Iyama and Yoshino
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 591-612
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Ideals of Herzog–Northcott type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 161-186
-
- Article
-
- You have access
- Export citation
ON THE STRUCTURE OF COMAXIMAL GRAPHS OF COMMUTATIVE RINGS WITH IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 26 November 2010, pp. 11-21
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON PRINCIPAL PRIME IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 130-137
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
The rank of a hypergeometric system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 284-318
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
An extension of Buchberger’s criteria for Gröbner basis decision
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 111-129
-
- Article
-
- You have access
- Export citation
On the adjoint quotient of Chevalley groups over arbitrary base schemes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 16 April 2010, pp. 673-704
- Print publication:
- October 2010
-
- Article
- Export citation
The semisimplicity conjecture for A-motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 561-598
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
A Characterization Related to the Equilibrium Distribution Associated with a Polynomial Structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 293-299
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Fibers of generic projections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 435-456
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
COFINITENESS AND FINITENESS OF GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 23 July 2009, pp. 244-250
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Gorenstein rings through face rings of manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 993-1000
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Cluster complexes via semi-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 1001-1034
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
COMMON FACTORS OF RESULTANTS MODULO p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 299-302
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Representations of Non-Negative Polynomials, Degree Bounds and Applications to Optimization
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 205-221
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
The Minimal Resolution Conjecture for Points on the Cubic Surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-49
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
ATTACHED PRIMES OF THE TOP GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 59-67
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
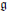 over an arbitrary base scheme
over an arbitrary base scheme 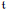 and associated Weyl group
and associated Weyl group 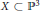
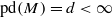 ,
, 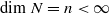 . First, we give the formula for the attached primes of the top generalized local cohomology module
. First, we give the formula for the attached primes of the top generalized local cohomology module 