Refine listing
Actions for selected content:
447 results in 13xxx
Hochschild cohomology, the characteristic morphism and derived deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1557-1580
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Hilbert’s 14th problem over finite fields and a conjecture on the cone of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1176-1198
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Oort groups and lifting problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 849-866
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Parameter-test-ideals of Cohen–Macaulay rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 933-948
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
IDEALS IN DIRECT PRODUCTS OF COMMUTATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 477-483
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Deformation of finite morphisms and smoothing of ropes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 673-688
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
A generalized Gaeta’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 689-704
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
STRONGLY IRREDUCIBLE IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 145-154
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
The Frobenius action on local cohomology modules in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1478-1492
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On the asymptotic behaviour of associated primes of generalized local cohomology modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-226
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Extending abelian groups to rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-314
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Relative amenability and the non-amenability of B(l1)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-333
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
About directed unions of Artinian subrings of a Von Neumann regular ring
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-304
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Quadratic polynomials, factorization in integral domains and Schreier domains from pullbacks
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-112
- Print publication:
- December 2003
-
- Article
- Export citation
A generalization of the cofiniteness problem in local cohomology modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-324
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
On The Asymptotic Values of Length Functions In Krull And Finitely Generated commutative Monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-436
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Hilbert function and fractional powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-75
- Print publication:
- June 2002
-
- Article
- Export citation
On the tensor product of polynomials over a ring
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-324
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Prüfer domains and pure submodules of direct sums of ideals
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 425-432
- Print publication:
- December 1999
-
- Article
- Export citation
The resultant and the Koszul complex of a set of forms
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 348-356
- Print publication:
- December 1997
-
- Article
- Export citation
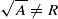 )), the Abelian group (
)), the Abelian group (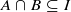 implies that either
implies that either 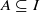 or
or 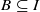 . In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.
. In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.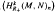 be the
be the 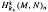 . In this paper we study the asymptotic behavior of Assf
. In this paper we study the asymptotic behavior of Assf 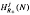 is not finitely generated.
is not finitely generated.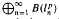 is no amenable for 1 ≤
is no amenable for 1 ≤ 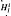 (
(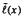 and
and 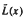 on
on 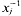 of degree - 1 be a formal inverse of
of degree - 1 be a formal inverse of 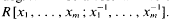 In [2, §2] we introduced a graded complex of
In [2, §2] we introduced a graded complex of 