We study the top left derived functors of the generalised 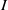$I$-adic completion and obtain equivalent properties concerning the vanishing or nonvanishing of the modules ${L}_{i} {\Lambda }_{I} (M, N)$. We also obtain some results for the sets $\text{Coass} ({L}_{i} {\Lambda }_{I} (M; N))$ and ${\text{Cosupp} }_{R} ({ H}_{i}^{I} (M; N))$.

We construct two bases for each cluster algebra coming from a triangulated surface without punctures. We work in the context of a coefficient system coming from a full-rank exchange matrix, such as principal coefficients.

Is the cohomology of the classifying space of a p-compact group, with Noetherian twisted coefficients, a Noetherian module? In this paper we provide, over the ring of p-adic integers, such a generalization to p-compact groups of the Evens–Venkov Theorem. We consider the cohomology of a space with coefficients in a module, and we compare Noetherianity over the field with p elements with Noetherianity over the p-adic integers, in the case when the fundamental group is a finite p-group.

To each tagged triangulation of a surface with marked points and non-empty boundary we associate a quiver with potential in such a way that whenever we apply a flip to a tagged triangulation the Jacobian algebra of the quiver with potential (QP) associated to the resulting tagged triangulation is isomorphic to the Jacobian algebra of the QP obtained by mutating the QP of the original one. Furthermore, we show that any two tagged triangulations are related by a sequence of flips compatible with QP-mutation. We also prove that, for each of the QPs constructed, the ideal of the non-completed path algebra generated by the cyclic derivatives is admissible and the corresponding quotient is isomorphic to the Jacobian algebra. These results, which generalize some of the second author’s previous work for ideal triangulations, are then applied to prove properties of cluster monomials, like linear independence, in the cluster algebra associated to the given surface by Fomin, Shapiro and Thurston (with an arbitrary system of coefficients).

We prove a conjecture of Kontsevich, which asserts that the iterations of the non-commutative rational map Fr:(x,y)→(xyx−1,(1+yr)x−1) are given by non-commutative Laurent polynomials with non-negative integer coefficients.

Let $R$ be a commutative ring. The regular digraph of ideals of $R$, denoted by $\Gamma (R)$, is a digraph whose vertex set is the set of all nontrivial ideals of $R$ and, for every two distinct vertices $I$ and $J$, there is an arc from $I$ to $J$ whenever $I$ contains a nonzero divisor on $J$. In this paper, we study the connectedness of $\Gamma (R)$. We also completely characterise the diameter of this graph and determine the number of edges in $\Gamma (R)$, whenever $R$ is a finite direct product of fields. Among other things, we prove that $R$ has a finite number of ideals if and only if $\mathrm {N}_{\Gamma (R)}(I)$ is finite, for all vertices $I$ in $\Gamma (R)$, where $\mathrm {N}_{\Gamma (R)}(I)$ is the set of all adjacent vertices to $I$ in $\Gamma (R)$.

We study the geometry underlying the difference between non-negative polynomials and sums of squares (SOS). The hypersurfaces that discriminate these two cones for ternary sextics and quaternary quartics are shown to be Noether–Lefschetz loci of K3 surfaces. The projective duals of these hypersurfaces are defined by rank constraints on Hankel matrices. We compute their degrees using numerical algebraic geometry, thereby verifying results due to Maulik and Pandharipande. The non-SOS extreme rays of the two cones of non-negative forms are parametrized, respectively, by the Severi variety of plane rational sextics and by the variety of quartic symmetroids.

Let $\mathcal S$ be a Serre subcategory of the category of $R$-modules, where $R$ is a commutative Noetherian ring. Let $\mathfrak a$ and $\mathfrak b$ be ideals of $R$ and let $M$ and $N$ be finite $R$-modules. We prove that if $N$ and $H^i_{\mathfrak a}(M,N)$ belong to $\mathcal S$ for all $i\lt n$ and if $n\leq \mathrm {f}$-$\mathrm {grad}({\mathfrak a},{\mathfrak b},N )$, then $\mathrm {Hom}_{R}(R/{\mathfrak b},H^n_{{\mathfrak a}}(M,N))\in \mathcal S$. We deduce that if either $H^i_{\mathfrak a}(M,N)$ is finite or $\mathrm {Supp}\,H^i_{\mathfrak a}(M,N)$ is finite for all $i\lt n$, then $\mathrm {Ass}\,H^n_{\mathfrak a}(M,N)$ is finite. Next we give an affirmative answer, in certain cases, to the following question. If, for each prime ideal ${\mathfrak {p}}$ of $R$, there exists an integer $n_{\mathfrak {p}}$ such that $\mathfrak b^{n_{\mathfrak {p}}} H^i_{\mathfrak a R_{\mathfrak {p}}}({M_{\mathfrak {p}}},{N_{\mathfrak {p}}})=0$ for every $i$ less than a fixed integer $t$, then does there exist an integer $n$ such that $\mathfrak b^nH^i_{\mathfrak a}(M,N)=0$ for all $i\lt t$? A formulation of this question is referred to as the local-global principle for the annihilation of generalised local cohomology modules. Finally, we prove that there are local-global principles for the finiteness and Artinianness of generalised local cohomology modules.

We show that the Hilbert scheme, that parameterizes all ideals with the same Hilbert function over a Clements–Lindström ring W, is connected. More precisely, we prove that every graded ideal is connected by a sequence of deformations to the lex-plus-powers ideal with the same Hilbert function. This is an analogue of Hartshorne’s theorem that Grothendieck’s Hilbert scheme is connected. We also prove a conjecture by Gasharov, Hibi, and Peeva that the lex ideal attains maximal Betti numbers among all graded ideals in W with a fixed Hilbert function.

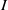
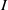
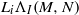
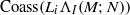
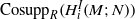
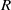
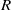
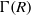
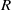
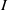
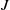
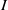
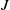
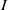
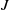
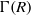
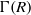
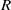
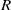
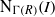
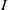
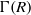
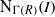
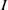
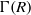
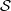
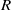
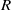
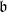
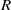
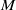
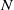
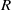
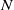
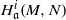
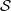
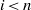
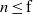
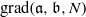
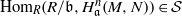
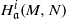
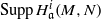
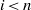
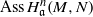
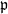
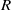
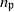
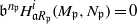
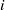
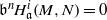
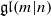
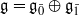Let be a classical Lie superalgebra and let ℱ be the category of finite-dimensional 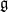-supermodules which are completely reducible over the reductive Lie algebra 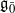. In [B. D. Boe, J. R. Kujawa and D. K. Nakano, 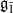Complexity and module varieties for classical Lie superalgebras, Int. Math. Res. Not. IMRN (2011), 696–724], we demonstrated that for any module M in ℱ the rate of growth of the minimal projective resolution (i.e. the complexity of M) is bounded by the dimension of . In this paper we compute the complexity of the simple modules and the Kac modules for the Lie superalgebra . In both cases we show that the complexity is related to the atypicality of the block containing the module.

Generalizing a result of Yoshinaga in dimension three, we show that a central hyperplane arrangement in 4-space is free exactly if its restriction with multiplicities to a fixed hyperplane of the arrangement is free and its reduced characteristic polynomial equals the characteristic polynomial of this restriction. We show that the same statement holds true in any dimension when imposing certain tameness hypotheses.

Suppose that W is a finite, unitary, reflection group acting on the complex vector space V and X is a subspace of V. Define N to be the setwise stabilizer of X in W, Z to be the pointwise stabilizer, and C=N/Z. Then restriction defines a homomorphism from the algebra of W-invariant polynomial functions on V to the algebra of C-invariant functions on X. In this note we consider the special case when W is a Coxeter group, V is the complexified reflection representation of W, and X is in the lattice of the arrangement of W, and give a simple, combinatorial characterization of when the restriction mapping is surjective in terms of the exponents of W and C. As an application of our result, in the case when W is the Weyl group of a semisimple, complex Lie algebra, we complete a calculation begun by Richardson in 1987 and obtain a simple combinatorial characterization of regular decomposition classes whose closure is a normal variety.

We define a hyperplane group to be a finite group generated by reflections fixing a single hyperplane pointwise. Landweber and Stong proved that the invariant ring of a hyperplane group is again a polynomial ring in any characteristic. Recently, Hartmann and Shepler gave a constructive proof of this result. By their algorithm, one can always construct generators that are additive. In this paper, we study hyperplane groups of order a power of a prime p in characteristic p and give a slightly different construction of the generators than Hartmann and Shepler. We then show that such generators have a particular form. 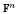Furthermore, we show that if the group is defined by a finite additive subgroup W ⊆ , the vanishing ideal of W is generated by polynomials obtained from a set of generators of the invariant ring that are additive. Finally, we give a shorter proof of the fact that the module of the invariant differential 1-forms is free in our situation.

A type of generalized higher derivation consisting of a collection of self-mappings of a ring associated with a monoid, and here called a D-structure, is studied. Such structures were previously used to define various kinds of ‘skew’ or ‘twisted’ monoid rings. We show how certain gradings by monoids define D-structures. The monoid ring defined by such a structure corresponding to a group-grading is the variant of the group ring introduced by Năstăsescu, while in the case of a cyclic group of order two, the form of the D-structure itself yields some gradability criteria of Bakhturin and Parmenter. A partial description is obtained of the D-structures associated with infinite cyclic monoids.

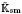We show that spaces of Colombeau generalized functions with smooth parameter dependence are isomorphic to those with continuous parametrization. Based on this result we initiate a systematic study of algebraic properties of the ring of generalized numbers in this unified setting. In particular, we investigate the ring and order structure of and establish some properties of its ideals.

Let (R,m) be a Noetherian local ring and UR=Spec(R)−{m} be the punctured spectrum of R. Gabber conjectured that if R is a complete intersection of dimension three, then the abelian group Pic(UR) is torsion-free. In this note we prove Gabber’s statement for the hypersurface case. We also point out certain connections between Gabber’s conjecture, Van den Bergh’s notion of non-commutative crepant resolutions and some well-studied questions in homological algebra over local rings.

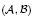We show that if the given cotorsion pair in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.

The Möbius inversion formula for a locally finite partially ordered set is realized as a Lagrange inversion formula. Schauder bases are introduced to interpret Möbius inversion.

In 1992, Göran Björck and Ralf Fröberg completely characterized the solution set of cyclic-8. In 2001, Jean-Charles Faugère determined the solution set of cyclic-9, by computer algebra methods and Gröbner basis computation. In this paper, a new theory in matrix analysis of rank-deficient matrices together with algorithms in numerical algebraic geometry enables us to present a symbolic-numerical algorithm to derive exactly the defining polynomials of all prime ideals of positive dimension in primary decomposition of cyclic-12. Empirical evidence together with rigorous proof establishes the fact that the positive-dimensional solution variety of cyclic-12 just consists of 72 quadrics of dimension one.

The paper deals with the classification of Leibniz central extensions of a filiform Lie algebra. We choose a basis with respect to which the multiplication table has a simple form. In low-dimensional cases isomorphism classes of the central extensions are given. In the case of parametric families of orbits, invariant functions (orbit functions) are provided.