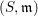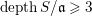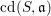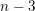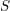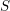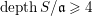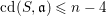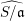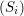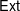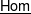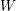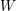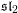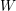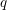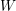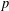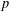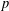Refine listing
Actions for selected content:
448 results in 13xxx
Elasticity in Polynomial-Type Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 28 March 2016, pp. 581-590
-
- Article
- Export citation
PROGRESS ON THE AUSLANDER–REITEN CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 433-440
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Application of Braiding Sequences. II. Polynomial Invariants of Positive Knots
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 1037-1064
-
- Article
- Export citation
ULRICH IDEALS AND MODULES OVER TWO-DIMENSIONAL RATIONAL SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 69-110
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
Homaloidal nets and ideals of fat points I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 54-77
-
- Article
-
- You have access
- Export citation
Upper semi-continuity of the Hilbert–Kunz multiplicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 477-488
- Print publication:
- March 2016
-
- Article
- Export citation
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 13 January 2016, pp. 171-206
- Print publication:
- February 2018
-
- Article
- Export citation
Zero-Separating Invariants for Linear Algebraic Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 911-924
-
- Article
- Export citation
On the relationship between depth and cohomological dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 876-888
- Print publication:
- April 2016
-
- Article
- Export citation
THE DIMENSION OF A SUBCATEGORY OF MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 09 October 2015, e19
-
- Article
-
- You have access
- Open access
- Export citation
The two-color Soergel calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 22 September 2015, pp. 327-398
- Print publication:
- February 2016
-
- Article
- Export citation
Torsion in tensor powers of modules
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 113-125
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
On modules of finite projective dimension
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 87-111
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
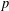 $p$-DIVISIBILITY FOR COHERENT COHOMOLOGY
$p$-DIVISIBILITY FOR COHERENT COHOMOLOGY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 13 August 2015, e15
-
- Article
-
- You have access
- Open access
- Export citation
EXPLICIT CONSTRUCTION OF COMPANION BASES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 357-384
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
ON THE WEAK GROTHENDIECK GROUP OF A BEZOUT RING
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 617-635
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
On the Canonical Ideals of One-Dimensional Cohen–Macaulay Local Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 13 July 2015, pp. 77-90
-
- Article
- Export citation
Some Homological Criteria for Regular, Complete Intersection and Gorenstein Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 473-481
-
- Article
- Export citation
STABILITY PATTERNS IN REPRESENTATION THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e11
-
- Article
-
- You have access
- Open access
- Export citation
Hilbert series of residual intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 09 June 2015, pp. 1663-1687
- Print publication:
- September 2015
-
- Article
- Export citation
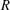
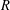
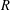

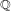
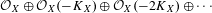


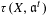
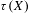

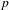
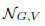 its null-cone. Let δ(
its null-cone. Let δ(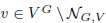 and
and 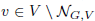 , respectively, there exists a homogeneous invariant
, respectively, there exists a homogeneous invariant