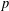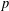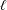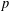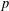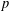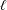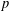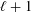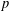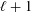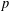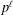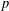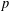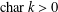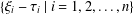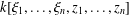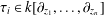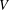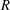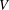Refine listing
Actions for selected content:
447 results in 13xxx
FROBENIUS ACTIONS ON LOCAL COHOMOLOGY MODULES AND DEFORMATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 07 September 2017, pp. 55-75
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE EFFECTIVE CONE OF MODULI SPACES OF SHEAVES ON A SMOOTH QUADRIC SURFACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 151-215
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
QUANTISATION SPACES OF CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 273-284
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
GRADED UNIPOTENT GROUPS AND GROSSHANS THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 04 September 2017, e21
-
- Article
-
- You have access
- Open access
- Export citation
THE SHORT RESOLUTION OF A SEMIGROUP ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 400-411
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Perfect complexes on algebraic stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 2318-2367
- Print publication:
- November 2017
-
- Article
- Export citation
Proof of de Smit’s conjecture: a freeness criterion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2310-2317
- Print publication:
- November 2017
-
- Article
- Export citation
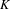 $K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
$K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 10 August 2017, pp. 1051-1085
- Print publication:
- September 2019
-
- Article
- Export citation
On the de Rham homology and cohomology of a complete local ring in equicharacteristic zero
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 2075-2146
- Print publication:
- October 2017
-
- Article
- Export citation
Local cohomology of Du Bois singularities and applications to families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2147-2170
- Print publication:
- October 2017
-
- Article
- Export citation
Invariants of GLn (𝔽q ) in polynomials modulo Frobenius powers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 831-873
- Print publication:
- August 2017
-
- Article
- Export citation
Tilting subcategories with respect to cotorsion triples in abelian categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 703-726
- Print publication:
- August 2017
-
- Article
- Export citation
ESSENTIAL DIMENSION OF GENERIC SYMBOLS IN CHARACTERISTIC
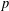 $p$
$p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 June 2017, e14
-
- Article
-
- You have access
- Open access
- Export citation
IMAGES OF HIGHER-ORDER DIFFERENTIAL OPERATORS OF POLYNOMIAL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 09 June 2017, pp. 205-211
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
CONGRUENCE OF SYMMETRIC INNER PRODUCTS OVER FINITE COMMUTATIVE RINGS OF ODD CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 389-397
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
LYUBEZNIK NUMBERS OF LOCAL RINGS AND LINEAR STRANDS OF GRADED IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 23-54
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE DOUBLE SHUFFLE RELATIONS FOR MULTIPLE EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 180-212
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Theta bases are atomic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1217-1219
- Print publication:
- June 2017
-
- Article
- Export citation
THE PROJECTIVE DIMENSION OF THE EDGE IDEAL OF A VERY WELL-COVERED GRAPH
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 160-179
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
A Convenient Notion of Compact Set for Generalized Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 03 April 2017, pp. 57-92
-
- Article
- Export citation
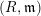
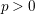
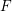
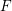
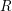
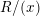
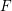
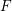
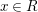
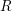
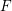
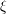
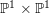
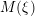
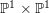
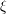
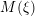
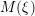
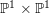
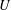
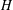

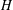
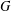
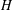

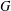
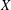
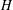
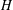
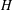
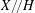
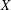
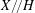
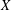
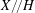
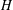
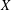
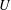
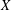
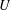
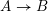
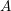
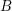
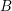
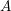
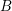
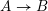
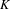
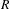
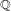
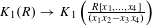
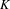
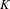
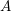
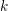
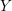
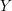
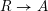
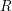
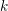
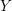
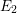
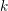
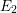
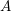
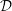
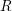
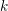
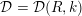
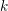
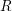
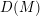
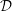
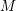
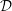
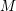
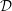
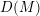
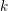
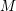
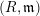
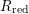
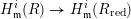
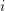
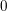
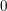
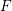
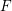
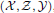 , the notion of
, the notion of 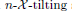 subcategories in an abelian category
subcategories in an abelian category 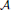 is introduced. It is proved that a virtually Gorenstein ring
is introduced. It is proved that a virtually Gorenstein ring 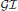 of Gorenstein injective
of Gorenstein injective 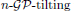 with respect to the cotorsion triple
with respect to the cotorsion triple 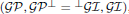 , where
, where 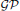 stands for the subcategory of Gorenstein projectives. In the case when a subcategory
stands for the subcategory of Gorenstein projectives. In the case when a subcategory 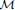 of
of 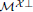 admits a right
admits a right 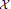 -coresolving covariantly finite and closed under direct summands.
-coresolving covariantly finite and closed under direct summands.