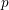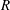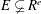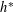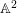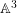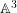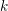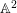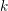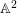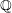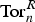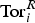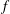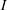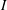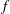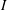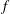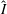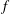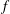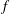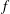Refine listing
Actions for selected content:
448 results in 13xxx
On local stabilities of
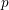 $p$-Kähler structures
$p$-Kähler structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 455-483
- Print publication:
- March 2019
-
- Article
- Export citation
On the Ideal Case of a Conjecture of Huneke and Wiegand
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 847-859
-
- Article
- Export citation
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Interlacing polynomials and the veronese construction for rational formal power series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1-16
- Print publication:
- February 2020
-
- Article
- Export citation
On triangle equivalences of stable categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 955-974
- Print publication:
- April 2020
-
- Article
- Export citation
On Deformations of Pairs (Manifold, Coherent Sheaf)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1209-1241
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On Special Fiber Rings of Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 225-242
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Degrees of Regular Sequences With a Symmetric Group Action
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 557-578
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
- Print publication:
- 2019
-
- Article
- Export citation
CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 27 December 2018, pp. 322-345
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Pólya S3-extensions of ℚ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1421-1433
- Print publication:
- December 2019
-
- Article
- Export citation
ON SEPARABLE
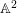 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 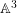 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 346-354
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Rigidity of Ext and Tor with Coefficients in Residue Fields of a Commutative Noetherian Ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 305-321
-
- Article
- Export citation
Newton Complementary Duals of
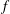 $f$-Ideals
$f$-Ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 231-241
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
VANISHING OF (CO)HOMOLOGY OVER DEFORMATIONS OF COHEN-MACAULAY LOCAL RINGS OF MINIMAL MULTIPLICITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 12 October 2018, pp. 705-725
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Foundations of Boij–Söderberg theory for Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 11 September 2018, pp. 2205-2238
- Print publication:
- October 2018
-
- Article
- Export citation
Line arrangements and configurations of points with an unexpected geometric property
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 2150-2194
- Print publication:
- October 2018
-
- Article
- Export citation
BETTI NUMBERS FOR CERTAIN COHEN–MACAULAY TANGENT CONES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 68-77
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Grothendieck–Plücker Images of Hilbert Schemes are Degenerate
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 47-60
-
- Article
- Export citation
On the Integral Degree of Integral Ring Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 25-46
-
- Article
- Export citation