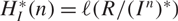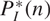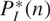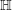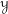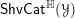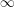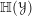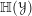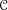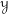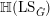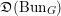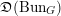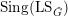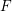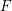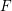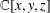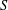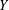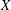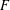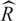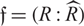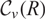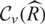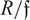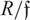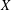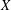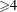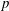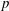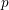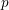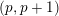Refine listing
Actions for selected content:
447 results in 13xxx
Spectra of Boolean Graphs Over Finite Fields of Characteristic Two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 58-65
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Laurent phenomenon and simple modules of quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2263-2295
- Print publication:
- December 2019
-
- Article
- Export citation
Residual intersections are Koszul–Fitting ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 23 September 2019, pp. 2150-2179
- Print publication:
- November 2019
-
- Article
- Export citation
THE GAMMA CONSTRUCTION AND ASYMPTOTIC INVARIANTS OF LINE BUNDLES OVER ARBITRARY FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 23 September 2019, pp. 165-207
- Print publication:
- June 2021
-
- Article
- Export citation
Poincaré duality and resonance varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 3001-3027
- Print publication:
- December 2020
-
- Article
- Export citation
INTEGRAL CLOSURE OF STRONGLY GOLOD IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 18 July 2019, pp. 204-216
- Print publication:
- March 2021
-
- Article
- Export citation
Tight closure of powers of ideals and tight hilbert polynomials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 335-355
- Print publication:
- September 2020
-
- Article
- Export citation
Sheaves of categories with local actions of Hochschild cochains
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1521-1567
- Print publication:
- August 2019
-
- Article
- Export citation
Affine cluster monomials are generalized minors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 14 June 2019, pp. 1301-1326
- Print publication:
- July 2019
-
- Article
- Export citation
Notes on linkage of modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1045-1062
-
- Article
- Export citation
An ideal-theoretic approach to Keller maps
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 June 2019, pp. 1033-1044
-
- Article
- Export citation
Ascending chain condition for
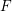 $F$-pure thresholds on a fixed strongly
$F$-pure thresholds on a fixed strongly 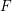 $F$-regular germ
$F$-regular germ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 28 May 2019, pp. 1194-1223
- Print publication:
- June 2019
-
- Article
- Export citation
Linear syzygies, hyperbolic Coxeter groups and regularity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1076-1097
- Print publication:
- June 2019
-
- Article
- Export citation
THE FACTORIAL CONJECTURE AND IMAGES OF LOCALLY NILPOTENT DERIVATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 20 May 2019, pp. 71-79
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
CLUSTER STRUCTURES ON HIGHER TEICHMULLER SPACES FOR CLASSICAL GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 May 2019, e13
-
- Article
-
- You have access
- Open access
- Export citation
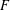 $F$-SIGNATURE UNDER BIRATIONAL MORPHISMS
$F$-SIGNATURE UNDER BIRATIONAL MORPHISMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, e11
-
- Article
-
- You have access
- Open access
- Export citation
ON THE ARITHMETIC OF MORI MONOIDS AND DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 313-322
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
OBSTRUCTIONS TO ALGEBRAIZING TOPOLOGICAL VECTOR BUNDLES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 21 March 2019, e6
-
- Article
-
- You have access
- Open access
- Export citation
Local Shtukas and Divisible Local Anderson Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1163-1207
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
On local stabilities of
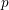 $p$-Kähler structures
$p$-Kähler structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 455-483
- Print publication:
- March 2019
-
- Article
- Export citation
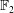
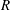
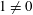
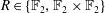
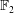
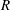
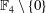
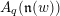
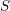
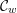
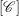
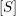
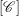
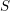
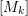
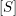
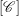
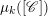
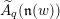
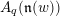
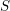
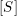
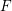
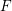
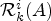
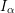
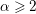
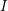
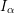
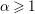
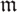 ) be an analytically unramified local ring of positive prime characteristic
) be an analytically unramified local ring of positive prime characteristic