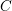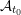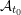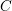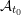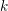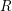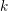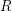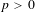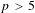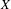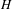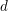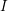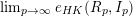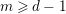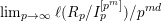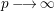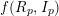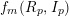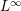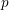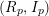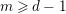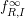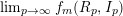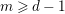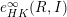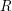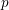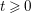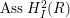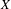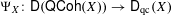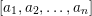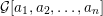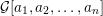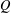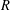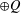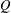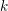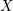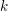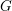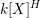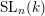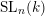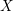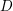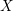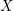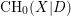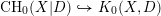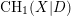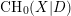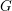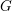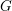Refine listing
Actions for selected content:
448 results in 13xxx
On the General Solution of the Heideman–Hogan Family of Recurrences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1113-1125
-
- Article
- Export citation
Bounding the Number of Common Zeros of Multivariate Polynomials and Their Consecutive Derivatives
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 August 2018, pp. 253-279
-
- Article
- Export citation
LIFTINGS OF A MONOMIAL CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 05 July 2018, pp. 230-238
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
A CONJECTURE ON
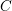 $C$-MATRICES OF CLUSTER ALGEBRAS
$C$-MATRICES OF CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 19 June 2018, pp. 37-46
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
DETECTING KOSZULNESS AND RELATED HOMOLOGICAL PROPERTIES FROM THE ALGEBRA STRUCTURE OF KOSZUL HOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 18 June 2018, pp. 47-85
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
GENERAL HYPERPLANE SECTIONS OF THREEFOLDS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 12 April 2018, pp. 647-661
- Print publication:
- March 2020
-
- Article
- Export citation
TOWARD HILBERT–KUNZ DENSITY FUNCTIONSIN CHARACTERISTIC 0
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 08 March 2018, pp. 158-200
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON THE ASSOCIATED PRIMES OF LOCAL COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 05 February 2018, pp. 1-9
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
NONINCREASING DEPTH FUNCTIONS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 505-511
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
ONE POSITIVE AND TWO NEGATIVE RESULTS FOR DERIVED CATEGORIES OF ALGEBRAIC STACKS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 22 January 2018, pp. 1087-1111
- Print publication:
- September 2019
-
- Article
- Export citation
Cluster algebras and continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 22 December 2017, pp. 565-593
- Print publication:
- March 2018
-
- Article
- Export citation
ON MODULES OVER COMMUTATIVE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 21 November 2017, pp. 341-356
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
CANONICAL LIFTS OF FAMILIES OFELLIPTIC CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 02 November 2017, pp. 193-213
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
THREE-DIMENSIONAL ISOLATED QUOTIENT SINGULARITIES IN EVEN CHARACTERISTIC
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 435-445
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
FACTORIZATION IN PRÜFER DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 401-409
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
NONNOETHERIAN HOMOTOPY DIMER ALGEBRAS AND NONCOMMUTATIVE CREPANT RESOLUTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 447-479
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
On the Popov–Pommerening conjecture for linear algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 36-79
- Print publication:
- January 2018
-
- Article
- Export citation
Zero cycles with modulus and zero cycles on singular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 120-187
- Print publication:
- January 2018
-
- Article
- Export citation
HYPERBOLIC 3-MANIFOLDS AND CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 28 September 2017, pp. 1-25
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON EXISTENCE OF CANONICAL
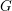 $G$-BASES
$G$-BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 15 September 2017, pp. 1-31
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation