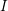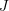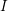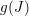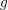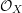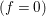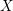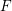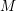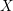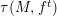Refine listing
Actions for selected content:
448 results in 13xxx
Supernatural analogues of Beilinson monads
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 14 November 2016, pp. 2545-2562
- Print publication:
- December 2016
-
- Article
- Export citation
A Study of the Length Function of Generalized Fractions of Modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 721-737
-
- Article
- Export citation
FIXED ELEMENTS OF NONINJECTIVE ENDOMORPHISMS OF POLYNOMIAL ALGEBRAS IN TWO VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 20 October 2016, pp. 209-213
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
WHEN IS THE INTEGRAL CLOSURE COMPARABLE TO ALL INTERMEDIATE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 14-21
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
LOCAL COHOMOLOGY OF MULTI-REES ALGEBRAS, JOINT REDUCTION NUMBERS AND PRODUCT OF COMPLETE IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 1-20
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
SALLY MODULES AND REDUCTION NUMBERS OF IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 106-126
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
THE STRUCTURE OF THE SALLY MODULE OF INTEGRALLY CLOSED IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 49-76
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
Degree bounds on homology and a conjecture of Derksen
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2041-2049
- Print publication:
- October 2016
-
- Article
- Export citation
BLOWUPS AND FIBERS OF MORPHISMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 13 September 2016, pp. 168-201
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
A TORSION-FREE ABELIAN GROUP EXISTS WHOSE QUOTIENT GROUP MODULO THE SQUARE SUBGROUP IS NOT A NIL-GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 449-456
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
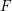 $F$ -PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
$F$ -PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 23 August 2016, pp. 10-36
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
The genus, Frobenius number and pseudo-Frobenius numbers of numerical semigroups of type 2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1081-1090
- Print publication:
- October 2016
-
- Article
- Export citation
THE
 ${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
Characters of equivariant
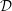 ${\mathcal{D}}$ -modules on spaces of matrices
${\mathcal{D}}$ -modules on spaces of matrices
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 28 June 2016, pp. 1935-1965
- Print publication:
- September 2016
-
- Article
- Export citation
Symbolic Powers of Monomial Ideals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 39-55
-
- Article
- Export citation
THE STRUCTURE OF BALANCED BIG COHEN–MACAULAY MODULES OVER COHEN–MACAULAY RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 549-561
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
HOMOTOPY THEORY OF MODULES AND ADAMS COCOMPLETION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 525-532
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
ON HILBERT FUNCTIONS OF GENERAL INTERSECTIONS OF IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 07 June 2016, pp. 61-73
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
BERNSTEIN–SATO POLYNOMIALS AND TEST MODULES IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 74-99
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
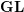
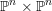
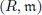 be a Noetherian local ring and let
be a Noetherian local ring and let 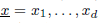 be a system of parameters of
be a system of parameters of 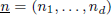 be a
be a 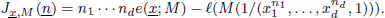
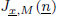 in the case in which
in the case in which 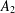
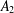
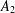
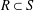
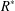
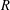
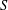
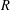
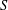
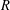
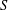
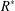
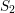
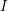
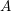
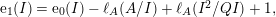
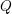
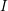
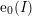
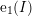
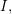
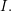
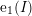
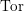
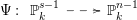 defined by homogeneous forms
defined by homogeneous forms 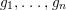
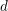
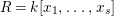
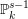
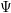
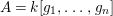
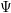
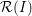
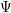
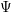
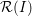
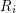
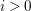
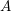
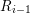
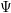
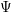
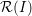
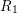
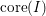
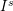
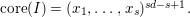
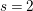
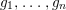
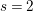
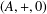
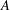
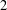
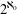
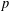
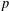
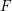
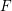
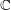
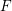
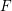
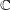
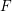

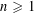
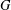
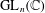
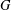
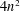
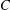
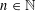
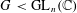
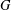
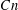

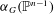
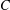
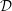
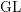
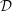
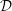
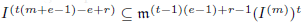 for all positive integers
for all positive integers 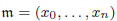 . This captures two conjectures (
. This captures two conjectures (