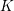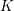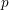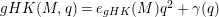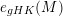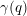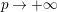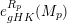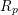Refine listing
Actions for selected content:
448 results in 13xxx
A Convenient Notion of Compact Set for Generalized Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 03 April 2017, pp. 57-92
-
- Article
- Export citation
ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 14 March 2017, pp. 705-715
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
On log del Pezzo surfaces in large characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 820-850
- Print publication:
- April 2017
-
- Article
- Export citation
ISOTONIAN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 March 2017, pp. 83-101
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
A CHARACTERISATION FOR A GROUPOID GALOIS EXTENSION USING PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 59-68
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Towards a symplectic version of the Chevalley restriction theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 647-666
- Print publication:
- March 2017
-
- Article
- Export citation
RELATIVE HILBERT CO-EFFICIENTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 729-741
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC TRIANGULATIONS AND COXETER TRANSFORMATIONS OF THE ANNULUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 27 February 2017, pp. 63-96
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
An intrinsic definition of the Rees algebra of a module
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 February 2017, pp. 13-30
-
- Article
- Export citation
ON THE ASYMPTOTIC BEHAVIOR OF THE LINEARITY DEFECT
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 20 February 2017, pp. 35-47
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
The extremal secant conjecture for curves of arbitrary gonality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 347-357
- Print publication:
- February 2017
-
- Article
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
LOCALLY ANALYTIC REPRESENTATIONS OF
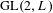 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 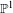 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 January 2017, pp. 125-187
- Print publication:
- January 2019
-
- Article
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
On Teter rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 125-139
- Print publication:
- February 2017
-
- Article
- Export citation
PARAMETRIC GEOMETRY OF NUMBERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1114-1135
- Print publication:
- 2017
-
- Article
- Export citation
A LOWER BOUND FOR THE GONALITY CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 561-563
- Print publication:
- 2017
-
- Article
- Export citation
A DESCENT THEOREM FOR FORMAL SMOOTHNESS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 08 December 2016, pp. 113-140
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
F-THRESHOLDS OF GRADED RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 07 December 2016, pp. 141-168
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
GENERALIZED HILBERT–KUNZ FUNCTION IN GRADED DIMENSION 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 05 December 2016, pp. 1-17
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
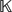
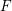
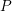
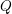
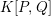
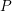
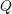
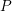
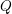
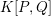
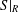
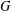
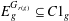
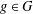
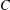
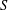
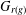
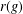
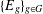
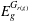
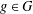
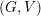

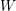
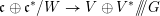
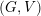
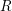
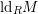
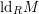
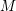
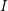
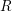
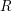
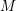
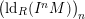
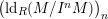
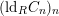
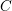
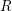
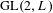
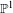
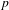

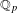
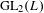
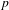
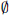 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.