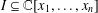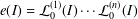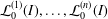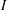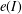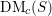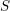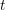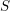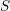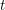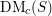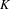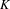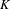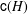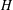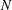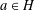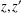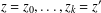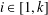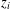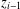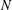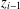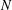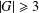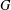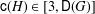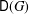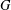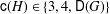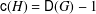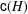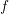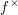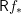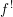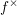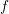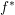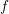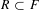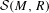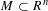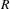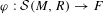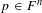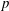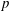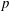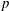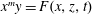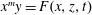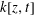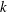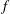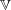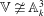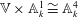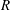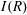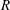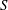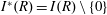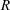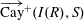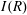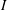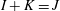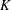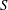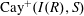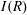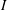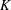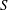Refine listing
Actions for selected content:
447 results in 13xxx
Generalized friezes and a modified Caldero–Chapoton map depending on a rigid object
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-124
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Bertini theorem for normality on local rings in mixed characteristic (applications to characteristic ideals)
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 125-173
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Purity for graded potentials and quantum cluster positivity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1913-1944
- Print publication:
- October 2015
-
- Article
- Export citation
de Rham cohomology of local cohomology modules: The graded case
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-21
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
MULTIPLICITY AND ŁOJASIEWICZ EXPONENT OF GENERIC LINEAR SECTIONS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 20 February 2015, pp. 191-201
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
VANISHING OF COHOMOLOGY OVER COMPLETE INTERSECTION RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 445-455
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
PRO CDH-DESCENT FOR CYCLIC HOMOLOGY AND
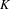 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 539-567
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Relation between two twisted inverse image pseudofunctors in duality theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 735-764
- Print publication:
- April 2015
-
- Article
- Export citation
Frobenius categories, Gorenstein algebras and rational surface singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 502-534
- Print publication:
- March 2015
-
- Article
- Export citation
DERIVED LOGARITHMIC GEOMETRY I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2014, pp. 367-405
- Print publication:
- April 2016
-
- Article
- Export citation
Koszul Complexes and Pole Order Filtrations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 333-354
-
- Article
-
- You have access
- Export citation
Corrigendum: Filtering free resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1482-1484
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Linear difference equations, frieze patterns, and the combinatorial Gale transform
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 22 August 2014, e22
-
- Article
-
- You have access
- Open access
- Export citation
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 128-147
-
- Article
-
- You have access
- Export citation
ON THE SUBSTITUTION THEOREM FOR RINGS OF SEMIALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 01 July 2014, pp. 857-894
- Print publication:
- October 2015
-
- Article
- Export citation
The
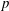 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
On the family of affine threefolds
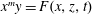 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 09 June 2014, pp. 979-998
- Print publication:
- June 2014
-
- Article
- Export citation
CAYLEY SUM GRAPHS OF IDEALS OF A COMMUTATIVE RING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 289-302
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
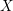
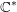
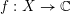
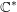
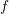
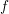
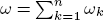 . Let
. Let 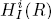 are holonomic (
are holonomic (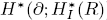 are concentrated in degree —
are concentrated in degree —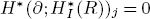 for
for 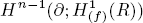 to
to