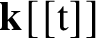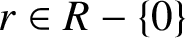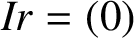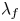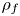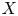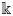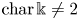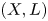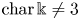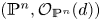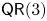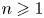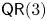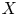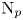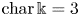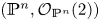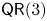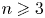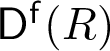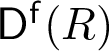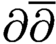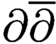Refine listing
Actions for selected content:
447 results in 13xxx
PRINCIPAL RADICAL SYSTEMS, LEFSCHETZ PROPERTIES, AND PERFECTION OF SPECHT IDEALS OF TWO-ROWED PARTITIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 690-730
- Print publication:
- September 2022
-
- Article
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear PDE with constant coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. S2-S27
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STRONG METRIC DIMENSION OF A TOTAL GRAPH OF NONZERO ANNIHILATING IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 431-439
- Print publication:
- June 2022
-
- Article
- Export citation
Geometric vertex decomposition and liaison
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 October 2021, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cluster Structures on Double Bott–Samelson Cells
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 September 2021, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Benson's cofibrants, Gorenstein projectives and a related conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 779-799
-
- Article
- Export citation
SOME STABLE NON-ELEMENTARY CLASSES OF MODULES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 93-117
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
De Rham–Witt sheaves via algebraic cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2089-2132
- Print publication:
- October 2021
-
- Article
- Export citation
Wiles defect for Hecke algebras that are not complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 16 August 2021, pp. 2046-2088
- Print publication:
- September 2021
-
- Article
- Export citation
Rank 3 quadratic generators of Veronese embeddings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 2001-2025
- Print publication:
- September 2021
-
- Article
- Export citation
Counterexamples to Hochschild-Kostant-Rosenberg in characteristic p
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 June 2021, e49
-
- Article
-
- You have access
- Open access
- Export citation
CONSTRUCTING NONPROXY SMALL TEST MODULES FOR THE COMPLETE INTERSECTION PROPERTY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 21 June 2021, pp. 412-429
- Print publication:
- June 2022
-
- Article
- Export citation
REPRESENTATION VARIETIES OF ALGEBRAS WITH NODES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2215-2245
- Print publication:
- November 2022
-
- Article
- Export citation
POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD
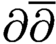 $\partial \overline {\partial }$-LEMMA
$\partial \overline {\partial }$-LEMMA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 305-354
- Print publication:
- June 2022
-
- Article
- Export citation
SIMPLICITY CRITERIA FOR RINGS OF DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 347-351
- Print publication:
- May 2022
-
- Article
- Export citation
THE METRIC DIMENSION OF THE ANNIHILATING-IDEAL GRAPH OF A FINITE COMMUTATIVE RING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 27 April 2021, pp. 362-368
- Print publication:
- June 2021
-
- Article
- Export citation
POWERS OF BINOMIAL EDGE IDEALS WITH QUADRATIC GRÖBNER BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 31 March 2021, pp. 233-255
- Print publication:
- June 2022
-
- Article
- Export citation
Depth-graded motivic multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 529-572
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation