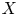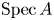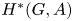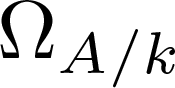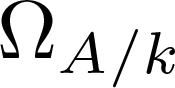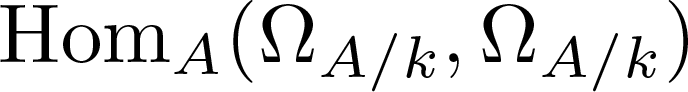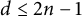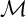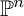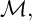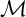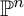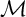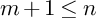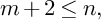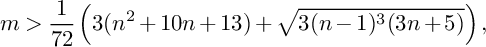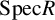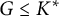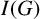Refine listing
Actions for selected content:
447 results in 13xxx
The Balmer spectrum of certain Deligne–Mumford stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1314-1346
- Print publication:
- June 2023
-
- Article
- Export citation
On one-dimensional local rings and Berger’s conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 437-452
-
- Article
- Export citation
Product decompositions of moment-angle manifolds and B-rigidity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1313-1325
- Print publication:
- December 2023
-
- Article
- Export citation
Gabber rigidity in hermitian K-theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 April 2023, pp. 1842-1847
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterisation of atomicity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-465
- Print publication:
- September 2023
-
- Article
- Export citation
Toric degenerations of low-degree hypersurfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1231-1236
- Print publication:
- December 2023
-
- Article
- Export citation
A CATEGORIFICATION OF ACYCLIC PRINCIPAL COEFFICIENT CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 22 February 2023, pp. 769-809
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation-finite quivers with real weights
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 February 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective freeness and stable rank of algebras of complex-valued BV functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 844-853
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On parabolic subgroups of symplectic reflection groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 401-413
- Print publication:
- May 2023
-
- Article
- Export citation
ANNIHILATORS AND DIMENSIONS OF THE SINGULARITY CATEGORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 533-548
- Print publication:
- June 2023
-
- Article
- Export citation
GENERIC LINES IN PROJECTIVE SPACE AND THE KOSZUL PROPERTY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 576-605
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on Hilbert–Kunz multiplicities and maximal F-signatures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 December 2022, pp. 247-271
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COSUPPORT FOR COMPACTLY GENERATED TRIANGULATED CATEGORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 13 December 2022, pp. 128-144
- Print publication:
- February 2024
-
- Article
- Export citation
ANALYTIC SPREAD OF FILTRATIONS ON TWO-DIMENSIONAL NORMAL LOCAL RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 239-268
- Print publication:
- March 2023
-
- Article
- Export citation
D-finite multivariate series with arithmetic restrictions on their coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1745-1779
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REGULARITY OF POWERS OF BIPARTITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1-9
- Print publication:
- February 2023
-
- Article
- Export citation
Bökstedt periodicity and quotients of DVRs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1683-1712
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calabi–Yau properties of Postnikov diagrams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation