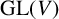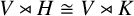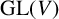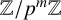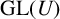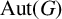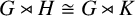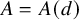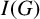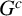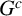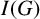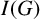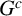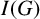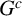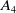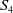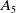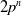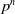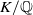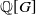Refine listing
Actions for selected content:
447 results in 13xxx
The Hilbert series of the superspace coinvariant ring
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 October 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 67-71
- Print publication:
- January 2025
-
- Article
- Export citation
ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 298-313
- Print publication:
- April 2025
-
- Article
- Export citation
Duality pairs, phantom maps, and definability in triangulated categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
Sums of squares, Hankel index and almost real rank
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 947-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 938-952
- Print publication:
- December 2024
-
- Article
- Export citation
ON THE SET OF BETTI ELEMENTS OF A PUISEUX MONOID
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 20 May 2024, pp. 80-92
- Print publication:
- February 2025
-
- Article
- Export citation
A short proof of the Hanlon-Hicks-Lazarev Theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilators and decompositions of singularity categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 23 April 2024, pp. 699-713
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBCOMPLEXES OF CERTAIN FREE RESOLUTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 886-904
- Print publication:
- December 2024
-
- Article
- Export citation
TILTING COMPLEXES AND CODIMENSION FUNCTIONS OVER COMMUTATIVE NOETHERIAN RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 618-693
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convexity of multiplicities of filtrations on local rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 878-914
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ideals with componentwise linear powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 833-841
- Print publication:
- September 2024
-
- Article
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1013-1040
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative rank and regularization
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING GEOMETRIC BRANCHES VIA THE FROBENIUS MAP AND F-NILPOTENT SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 724-741
- Print publication:
- September 2024
-
- Article
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 291-302
- Print publication:
- October 2024
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
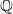 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation