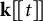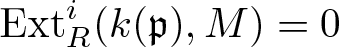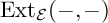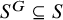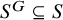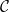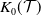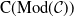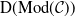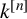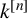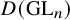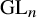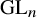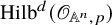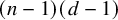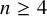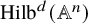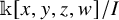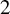Refine listing
Actions for selected content:
447 results in 13xxx
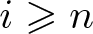
How to determine a curve singularity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 09 January 2024, pp. 633-647
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORMALLY REGULAR RINGS AND DESCENT OF REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 2279-2318
- Print publication:
- September 2024
-
- Article
- Export citation
DILOGARITHM IDENTITIES IN CLUSTER SCATTERING DIAGRAMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 1-22
- Print publication:
- March 2024
-
- Article
- Export citation
Lim Ulrich sequences and Boij-Söderberg cones
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Persistence and the Sheaf-Function Correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOW TO EXTEND CLOSURE AND INTERIOR OPERATIONS TO MORE MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 513-560
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical invariants for binary quintics and reduction types of Picard curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 65-87
- Print publication:
- January 2024
-
- Article
- Export citation
CODIMENSION ONE FOLIATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1705-1750
- Print publication:
- July 2024
-
- Article
- Export citation
Rigidity of Ext and Tor via flat–cotorsion theory
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1142-1153
-
- Article
- Export citation
Double Schubert polynomials do have saturated Newton polytopes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the reducing projective dimension over local rings
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 104-118
- Print publication:
- January 2024
-
- Article
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
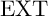 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A VARIANT OF PERFECTOID ABHYANKAR’S LEMMA AND ALMOST COHEN–MACAULAY ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 164-215
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ulrich modules and weakly lim Ulrich sequences do not always exist
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 August 2023, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
When are the natural embeddings of classical invariant rings pure?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poincaré complex diagonals and the Bass trace conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1819-1840
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized tilting theory in functor categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 595-611
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LND CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 412-421
- Print publication:
- December 2023
-
- Article
- Export citation
Multiple generalized cluster structures on
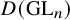 $D(\mathrm {GL}_n)$
$D(\mathrm {GL}_n)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 June 2023, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small elementary components of Hilbert schemes of points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 June 2023, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation