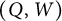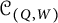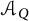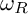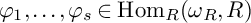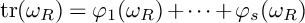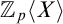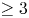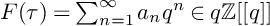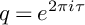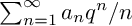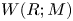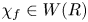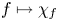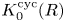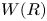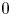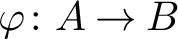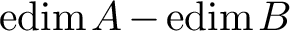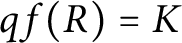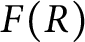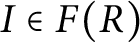Refine listing
Actions for selected content:
447 results in 13xxx
Maximum likelihood estimation for tensor normal models via castling transforms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 01 July 2022, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quivers with potentials for Grassmannian cluster algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1199-1225
- Print publication:
- August 2023
-
- Article
- Export citation
RINGS OF TETER TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 1005-1033
- Print publication:
- December 2022
-
- Article
- Export citation
Uniform Properties of Ideals in Rings of Restricted Power Series
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, p. 258
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
New examples of non-Fourier–Mukai functors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 1254-1267
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Casting light on shadow Somos sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. S87-S101
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABILITY OF HENSELIAN VALUATIONS BY CONDITIONS ON THE VALUE GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1064-1082
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL HILBERT COEFFICIENTS AND ELLIPTIC IDEALS IN NORMAL TWO-DIMENSIONAL SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 779-800
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert rings with maximal ideals of different heights and unruly Hilbert rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 196-203
- Print publication:
- March 2023
-
- Article
- Export citation
On Lipschitz normally embedded complex surface germs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 623-653
- Print publication:
- March 2022
-
- Article
- Export citation
The spectrum of a localic semiring
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 647-668
- Print publication:
- November 2022
-
- Article
- Export citation
Embedding codimension of the space of arcs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 February 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTINUOUS QUIVERS OF TYPE A (III) EMBEDDINGS OF CLUSTER THEORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 653-689
- Print publication:
- September 2022
-
- Article
- Export citation
Witt vectors with coefficients and characteristic polynomials over non-commutative rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 366-408
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A uniform treatment of Grothendieck's localization problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 57-88
- Print publication:
- January 2022
-
- Article
- Export citation
Bi-graded Koszul modules, K3 carpets, and Green's conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 33-56
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting G-Dedekind domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 38-52
- Print publication:
- March 2023
-
- Article
- Export citation