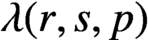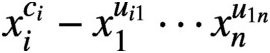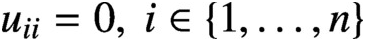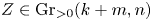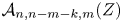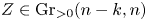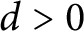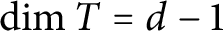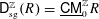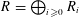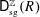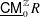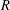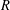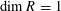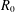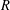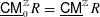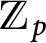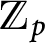Refine listing
Actions for selected content:
447 results in 13xxx
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
A NEW ALGORITHM FOR DECOMPOSING MODULAR TENSOR PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 94-107
- Print publication:
- August 2021
-
- Article
- Export citation
BOUNDS FOR INDEXES OF NILPOTENCY IN COMMUTATIVE RING THEORY: A PROOF MINING APPROACH
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 05 January 2021, pp. 257-267
- Print publication:
- December 2020
-
- Article
- Export citation
Equivariant cohomology of torus orbifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 299-328
- Print publication:
- April 2022
-
- Article
- Export citation
CRITICAL BINOMIAL IDEALS OF NORTHCOTT TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 48-70
- Print publication:
- February 2021
-
- Article
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
- Print publication:
- June 2021
-
- Article
- Export citation
ANALYTIC SPREAD AND INTEGRAL CLOSURE OF INTEGRALLY DECOMPOSABLE MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 03 November 2020, pp. 166-191
- Print publication:
- March 2022
-
- Article
- Export citation
Parity duality for the amplituhedron
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 09 December 2020, pp. 2207-2262
- Print publication:
- November 2020
-
- Article
- Export citation
Relations between modular invariants of a vector and a covector in dimension two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 820-827
- Print publication:
- December 2021
-
- Article
- Export citation
ERRATUM: CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 23 October 2020, pp. 229-231
- Print publication:
- March 2022
-
- Article
- Export citation
UNIFORM DEFINABILITY OF INTEGERS IN REDUCED INDECOMPOSABLE POLYNOMIAL RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1376-1402
- Print publication:
- December 2020
-
- Article
- Export citation
Toric degenerations of cluster varieties and cluster duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 07 December 2020, pp. 2149-2206
- Print publication:
- October 2020
-
- Article
- Export citation
ON THE DEPTH OF SYMBOLIC POWERS OF EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 28-40
- Print publication:
- March 2022
-
- Article
- Export citation
Constructing Fano 3-folds from cluster varieties of rank 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 09 November 2020, pp. 1873-1914
- Print publication:
- September 2020
-
- Article
- Export citation
LINEAR RELATIONS AND INTEGRABILITY FOR CLUSTER ALGEBRAS FROM AFFINE QUIVERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 584-621
- Print publication:
- September 2021
-
- Article
- Export citation
THE COMBINATORICS OF TENSOR PRODUCTS OF HIGHER AUSLANDER ALGEBRAS OF TYPE A
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 526-546
- Print publication:
- September 2021
-
- Article
- Export citation
Almost Gorenstein rings arising from fiber products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 383-400
- Print publication:
- June 2021
-
- Article
- Export citation
TILTING THEORY FOR GORENSTEIN RINGS IN DIMENSION ONE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 July 2020, e36
-
- Article
-
- You have access
- Open access
- Export citation
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation
Bounding the Iwasawa invariants of Selmer groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1390-1422
- Print publication:
- October 2021
-
- Article
- Export citation