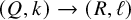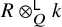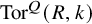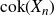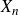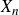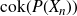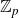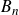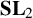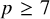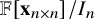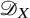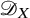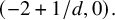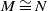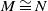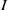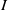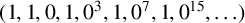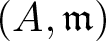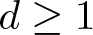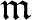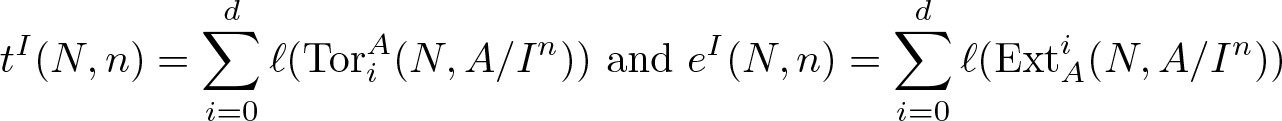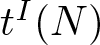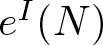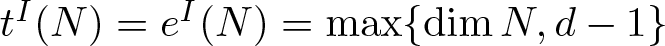Refine listing
Actions for selected content:
447 results in 13xxx
Koszul homomorphisms and universal resolutions in local algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 March 2025, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GAGA FOR HENSELIAN SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1547-1589
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The cokernel of a polynomial push-forward of a random integral matrix with concentrated residue
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 229-257
- Print publication:
- March 2025
-
- Article
- Export citation
TENSOR PRODUCTS OF d-FOLD MATRIX FACTORIZATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ASYMPTOTIC BEHAVIOR OF THE VASCONCELOS INVARIANT FOR GRADED MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 296-310
- Print publication:
- June 2025
-
- Article
- Export citation
THE DENSE REGION IN SCATTERING DIAGRAMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 290-302
- Print publication:
- October 2025
-
- Article
- Export citation
Deformations of morphisms of sheaves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On class groups of upper cluster algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL COHOMOLOGY UNDER SMALL PERTURBATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 183-200
- Print publication:
- June 2025
-
- Article
- Export citation
FORMAL LIFTING OF DUALIZING COMPLEXES AND CONSEQUENCES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 219-236
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivalences of stable categories of Gorenstein local rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 338-348
- Print publication:
- March 2025
-
- Article
- Export citation
On the gluing of germs of complex analytic spaces, Betti numbers, and their structure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 582-597
- Print publication:
- June 2025
-
- Article
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A power structure over the Grothendieck ring of geometric dg categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 05 December 2024, pp. 300-318
-
- Article
- Export citation
On split quasi-hereditary covers and Ringel duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Increasing subsequences, matrix loci and Viennot shadows
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
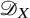 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 30 October 2024, pp. 86-106
- Print publication:
- January 2025
-
- Article
- Export citation
ON THE BINARY SEQUENCE
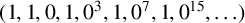 $(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
$(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 October 2024, pp. 260-271
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived functors and Hilbert polynomials over regular local rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1137-1147
-
- Article
- Export citation