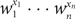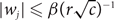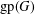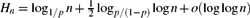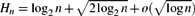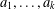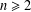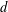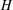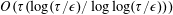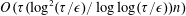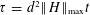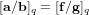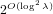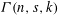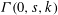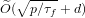Refine listing
Actions for selected content:
124 results in 68Qxx
Weighted counting of solutions to sparse systems of equations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 15 April 2019, pp. 696-719
-
- Article
- Export citation
Abelian Logic Gates
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 13 March 2019, pp. 388-422
-
- Article
- Export citation
Merge Decompositions, Two-sided Krohn–Rhodes, and Aperiodic Pointlikes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 199-208
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 388-391
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Polynomial Mixing of the Edge-Flip Markov Chain for Unbiased Dyadic Tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 365-387
-
- Article
- Export citation
Dual-Pivot Quicksort: Optimality, Analysis and Zeros of Associated Lattice Paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 14 August 2018, pp. 485-518
-
- Article
- Export citation
A GENERAL POSITION PROBLEM IN GRAPH THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 177-187
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Asymmetric Rényi Problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 27 June 2018, pp. 542-573
-
- Article
- Export citation
ON SEMIGROUPS WITH PSPACE-COMPLETE SUBPOWER MEMBERSHIP PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 127-142
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
COMPLEXITY OF SHORT GENERATING FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, e1
-
- Article
-
- You have access
- Open access
- Export citation
A Simple SVD Algorithm for Finding Hidden Partitions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 124-140
-
- Article
- Export citation
EXPONENTIAL IMPROVEMENT IN PRECISION FOR SIMULATING SPARSE HAMILTONIANS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 02 March 2017, e8
-
- Article
-
- You have access
- Open access
- Export citation
Bit flipping and time to recover
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 650-666
- Print publication:
- September 2016
-
- Article
- Export citation
Reduced memory meet-in-the-middle attackagainst the NTRU private key
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 43-57
-
- Article
-
- You have access
- Export citation
An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low-level encoding of zero
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 255-266
-
- Article
-
- You have access
- Export citation
CONSISTENCY OF CIRCUIT EVALUATION, EXTENDED RESOLUTION AND TOTAL NP SEARCH PROBLEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 24 June 2016, e15
-
- Article
-
- You have access
- Open access
- Export citation
On a Class of Automaton Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 31-38
-
- Article
- Export citation
Inapproximability of the Partition Function for the Antiferromagnetic Ising and Hard-Core Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 500-559
-
- Article
- Export citation
Nearly Optimal Bernoulli Factories for Linear Functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 577-591
-
- Article
- Export citation
A new approach to the discrete logarithm problem with auxiliary inputs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 January 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation