Refine listing
Actions for selected content:
124 results in 68Qxx
The Multiple-Orientability Thresholds for Random Hypergraphs†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 28 December 2015, pp. 870-908
-
- Article
- Export citation
Two compact incremental prime sieves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 November 2015, pp. 675-683
-
- Article
-
- You have access
- Export citation
The Satisfiability Threshold for k-XORSAT
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 31 July 2015, pp. 236-268
-
- Article
- Export citation
A THEORY OF COMPLEXITY, CONDITION, AND ROUNDOFF
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 27 February 2015, e4
-
- Article
-
- You have access
- Open access
- Export citation
McCammond’s normal forms for free aperiodic semigroups revisited
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 January 2015, pp. 130-147
-
- Article
-
- You have access
- Export citation
Coherent presentations of Artin monoids
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 957-998
- Print publication:
- May 2015
-
- Article
- Export citation
Computational Complexity of Topological Invariants
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 11 December 2014, pp. 27-32
-
- Article
-
- You have access
- Export citation
On the Nearest-Neighbor Algorithm for the Mean-Field Traveling Salesman Problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 106-117
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Probabilistic Cellular Automata, Invariant Measures, and Perfect Sampling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 960-980
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
On the use of expansion series for stream ciphers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 326-340
-
- Article
-
- You have access
- Export citation
On ε-Optimality of the Pursuit Learning Algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 795-805
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Testing commutativity of a group and the power of randomization
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 38-43
-
- Article
-
- You have access
- Export citation
Gröbner bases for quadratic algebras of skew type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 387-401
-
- Article
-
- You have access
- Export citation
Muller condition and fairness on multitransition systems
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 99-107
-
- Article
-
- You have access
- Export citation
Growth in Baumslag–Solitar groups I: subgroups and rationality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 34-71
-
- Article
-
- You have access
- Export citation
Constructing maximal subgroups of orthogonal groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 May 2010, pp. 164-191
-
- Article
-
- You have access
- Export citation
Une dualité entre fonctions booléennes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 633-652
- Print publication:
- July 2010
-
- Article
- Export citation
A Stochastic Maximin Fixed-Point Equation Related to Game Tree Evaluation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 586-606
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Monte Carlo Algorithms for Finding the Maximum of a Random Walk with Negative Drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 74-86
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A mosaic of triangular cells formed with sequential splitting rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 3-15
- Print publication:
- 2004
-
- Article
- Export citation






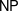

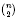 quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FM
quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FM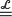 ξ max
ξ max