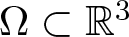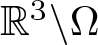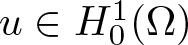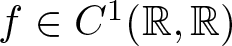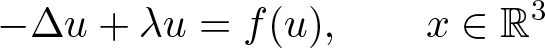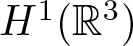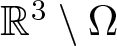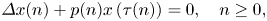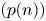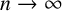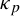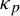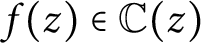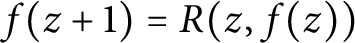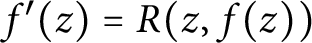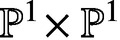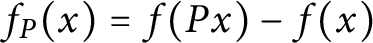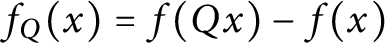Refine listing
Actions for selected content:
56 results in 39-XX
Twenty dry Martinis for the unitary almost-Mathieu operator
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A study of transcendental entire solutions of several nonlinear partial differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1329-1369
-
- Article
- Export citation
ANALYSIS OF A DISCRETIZED FRACTIONAL-ORDER PREY–PREDATOR MODEL UNDER WIND EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Time almost periodicity for solutions of Toda lattice equation with almost periodic initial datum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2561-2600
- Print publication:
- August 2025
-
- Article
- Export citation
Propagation dynamics for an epidemic patch model with variable incubation period
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 18 December 2024, pp. 948-971
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
General theorems for uniform asymptotic stability and boundedness in finitely delayed difference systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 May 2024, pp. 1046-1058
- Print publication:
- December 2024
-
- Article
- Export citation
(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1463-1484
- Print publication:
- December 2024
-
- Article
- Export citation
THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 145-154
- Print publication:
- August 2024
-
- Article
- Export citation
Discrete heat equation with irregular thermal conductivity and tempered distributional data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 September 2023, pp. 57-80
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of positive solutions for Kirchhoff-type problem in exterior domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 182-217
-
- Article
- Export citation
RECURSIVE CHARACTERISATIONS OF RANDOM MATRIX ENSEMBLES AND ASSOCIATED COMBINATORIAL OBJECTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 342-343
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Upper and lower limit oscillation conditions for first-order difference equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 July 2022, pp. 618-631
-
- Article
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation
Jump phenomena of the n-th eigenvalue of discrete Sturm–Liouville problems with application to the continuous case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 619-653
- Print publication:
- April 2023
-
- Article
- Export citation
APÉRY LIMITS FOR ELLIPTIC
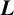 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chaotic behavior of the p-adic Potts–Bethe mapping II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3433-3457
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective finiteness of solutions to certain differential and difference equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 52-67
- Print publication:
- March 2022
-
- Article
- Export citation
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
- Print publication:
- June 2021
-
- Article
- Export citation
Criteria for periodicity and an application to elliptic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 530-540
- Print publication:
- September 2021
-
- Article
- Export citation
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation