Given a weakly almost additive sequence of continuous functions with bounded variation ${\mathcal {F}}=\{\log f_n\}_{n=1}^{\infty }$ on a subshift X over finitely many symbols, we study properties of a function f on X such that $\lim _{n\to \infty }({1}/{n})\int \log f_n\,d\mu =\int f\,d\mu $ for every invariant measure $\mu $ on X. Under some conditions, we construct a function f on X explicitly, and study a relation between the property of ${\mathcal {F}}$ and some particular types of f. As applications, we study images of Gibbs measures for continuous functions under one-block factor maps. We investigate a relation between the almost additivity of the sequences associated to relative pressure functions and the fiber-wise sub-positive mixing property of a factor map. For a special type of one-block factor maps between shifts of finite type, we study necessary and sufficient conditions for the image of a one-step Markov measure to be a Gibbs measure for a continuous function.

In this paper, we study the quantitative recurrence properties in the case of $\mathbb {Z}$-extension of Axiom A flows on a Riemannian manifold. We study the asymptotic behavior of the first return time to a small neighborhood of the starting point. We establish results of almost everywhere convergence, and of convergence in distribution with respect to any probability measure absolutely continuous with respect to the infinite invariant measure. In particular, our results apply to geodesic flows on the $\mathbb {Z}$-cover of compact smooth surfaces of negative curvature.

We prove that when the Aubry set for a Lipschitz continuous potential is a subshift of finite type, then the pressure function converges exponentially fast to its asymptote as the temperature goes to 0. The speed of convergence turns out to be the unique eigenvalue for the matrix whose entries are the costs between the different irreducible pieces of the Aubry set. For a special case of Walters potential, we show that perturbations of that potential that go faster to zero than the pressure do not change the selection, neither for the subaction nor for the limit measure, a zero temperature.

We prove that a partially hyperbolic attracting set for a $C^2$ vector field, having slow recurrence to equilibria, supports an ergodic physical/SRB measure if, and only if, the trapping region admits non-uniform sectional expansion on a positive Lebesgue measure subset. Moreover, in this case, the attracting set supports at most finitely many ergodic physical/SRB measures, which are also Gibbs states along the central-unstable direction. This extends to continuous time systems a similar well-known result obtained for diffeomorphisms, encompassing the presence of equilibria accumulated by regular orbits within the attracting set. In codimension two the same result holds, assuming only the trajectories on the trapping region admit a sequence of times with asymptotical sectional expansion, on a positive volume subset. We present several examples of application, including the existence of physical measures for asymptotically sectional hyperbolic attracting sets, and obtain physical measures in an alternative unified way for many known examples: Lorenz-like and Rovella attractors, and sectional-hyperbolic attracting sets (including the multidimensional Lorenz attractor).

In this article, we consider a closed rank-one Riemannian manifold M without focal points. Let $P(t)$ be the set of free-homotopy classes containing a closed geodesic on M with length at most t, and $\# P(t)$ its cardinality. We obtain the following Margulis-type asymptotic estimates:

$$ \begin{align*}\lim_{t\to \infty}\#P(t)/\frac{e^{ht}}{ht}=1\end{align*} $$

The marked length spectrum (MLS) of a closed negatively curved manifold $(M, g)$ is known to determine the metric g under various circumstances. We show that, in these cases, (approximate) values of the MLS on a sufficiently large finite set approximately determine the metric. Our approach is to recover the hypotheses of our main theorems in Butt [Quantative marked length spectrum rigidity. Preprint, 2022], namely, multiplicative closeness of the MLS functions on the entire set of closed geodesics of M. We use mainly dynamical tools and arguments, but take great care to show that the constants involved depend only on concrete geometric information about the given Riemannian metrics, such as the dimension, diameter and sectional curvature bounds.

We prove that among the set of pairs ($C^2$-diffeomorphism, $C^1$-potential), there exists a $C^1$-open and dense subset such that either the Lagrange spectrum is finite and the dynamics is a Morse–Smale diffeomorphism or the Lagrange spectrum has positive Hausdorff dimension and the system has positive topological entropy. We also prove that such dichotomy does not hold for typical systems when replacing the Lagrange by the Markov spectrum.

We study discretized Landau–de Gennes gradient dynamics of finite lattices and graphs in the small intersite coupling regime (“anticontinuous limit”). We consider the case of $3 \times 3$ Q-tensor systems and extend recent results on small coupling intersite equilibria to the case of geometries without boundaries. We show that the equation for Landau–de Gennes equilibria is reduced to an $SO(3)-$equivariant equation on submanifolds that are diffeomorphic to products of projective planes and are parametrized by uniaxial Q-tensors. The gradient flow of the Landau–de Gennes energy has a normally hyperbolic invariant attracting submanifold that is also parametrized by uniaxial Q-tensors. We also present numerical studies of the Landau–de Gennes gradient flow in open and periodic chain geometries. We see a rapid approach to a near-uniaxial state at each site, as expected by the theory, and a much slower decay to an equilibrium configuration. The long time scale is several orders of magnitudes slower, and can depend on the size of the lattice and the initial condition. In the case of the circle we see evidence for two stable equilibria that are discrete analogues of curves belonging to the two homotopy classes of the projective plane. Evidence of bistability is also seen numerically in the open chain geometry.

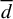For full shifts on finite alphabets, Coelho and Quas [Criteria for $\overline {d}$-continuity. Trans. Amer. Math. Soc. 350(8) (1998), 3257–3268] showed that the map that sends a Hölder continuous potential $\phi $ to its equilibrium state $\mu _\phi $ is $\overline {d}$-continuous. We extend this result to the setting of full shifts on countable (infinite) alphabets. As part of the proof, we show that the map that sends a strongly positive recurrent potential to its normalization is continuous for potentials on mixing countable state Markov shifts.

In this paper, we give a complete topological and smooth classification of non-invertible Anosov maps on torus. We show that two non-invertible Anosov maps on torus are topologically conjugate if and only if their corresponding periodic points have the same Lyapunov exponents on the stable bundles. As a corollary, if two $C^r$ non-invertible Anosov maps on torus are topologically conjugate, then the conjugacy is $C^r$-smooth along the stable foliation. Moreover, we show that the smooth conjugacy class of a non-invertible Anosov map on torus is completely determined by the Jacobians of return maps at periodic points.

In this paper, we show that for any nonautonomous discrete time dynamical system in a Banach space if its linear part has a dichotomy and the composition of a generalized Green function and the nonlinear term of the system has a weighted integrable Lipschitz constant then the system has the weighted Lipschitz shadowing property for a type of weighted pseudo orbits in the whole phase space. Additionally, if the generalized Green function is the Green function for the dichotomy and the evolution operator restricted to the stable subspace (resp. unstable subspace) tends to 0 in weight as time tends to $+\infty$ (resp. $-\infty$) then the system has the weighted generalized forward (resp. backward) limit shadowing property. By the same approach we prove that a C1 map with a compact hyperbolic invariant set has the weighted Lipschitz shadowing property and the generalized weighted limit shadowing property for weighted pseudo orbits in the hyperbolic set. We also give the parallel results for differential equations.

We compare the marked length spectra of some pairs of proper and cocompact cubical actions of a nonvirtually cyclic group on $\mathrm {CAT}(0)$ cube complexes. The cubulations are required to be virtually co-special, have the same sets of convex-cocompact subgroups, and admit a contracting element. There are many groups for which these conditions are always fulfilled for any pair of cubulations, including nonelementary cubulable hyperbolic groups, many cubulable relatively hyperbolic groups, and many right-angled Artin and Coxeter groups.

For these pairs of cubulations, we study the Manhattan curve associated to their combinatorial metrics. We prove that this curve is analytic and convex, and a straight line if and only if the marked length spectra are homothetic. The same result holds if we consider invariant combinatorial metrics in which the lengths of the edges are not necessarily one. In addition, for their standard combinatorial metrics, we prove a large deviations theorem with shrinking intervals for their marked length spectra. We deduce the same result for pairs of word metrics on hyperbolic groups.

The main tool is the construction of a finite-state automaton that simultaneously encodes the marked length spectra of both cubulations in a coherent way, in analogy with results about (bi)combable functions on hyperbolic groups by Calegari-Fujiwara [14]. The existence of this automaton allows us to apply the machinery of thermodynamic formalism for suspension flows over subshifts of finite type, from which we deduce our results.

For continuous self-maps of compact metric spaces, we explore the relationship among the shadowable points, sensitive points, and entropy points. Specifically, we show that (1) if the set of shadowable points is dense in the phase space, then any interior point of the set of sensitive points is an entropy point; and (2) if the topological entropy is zero, then the denseness of the set of shadowable points is equivalent to almost chain continuity. In addition, we present a counter-example to a question raised by Ye and Zhang regarding entropy points.

In this paper, we consider a class of affine Anosov mappings with a quasi-periodic forcing and show that there is a unique positive integer m, which only depends on the system, such that the exponential growth rate of the number of invariant tori of degree m is equal to the topological entropy.

Let $ K $ be a compact subset of the d-torus invariant under an expanding diagonal endomorphism with s distinct eigenvalues. Suppose the symbolic coding of K satisfies weak specification. When $ s \leq 2 $, we prove that the following three statements are equivalent: (A) the Hausdorff and box dimensions of $ K $ coincide; (B) with respect to some gauge function, the Hausdorff measure of $ K $ is positive and finite; (C) the Hausdorff dimension of the measure of maximal entropy on $ K $ attains the Hausdorff dimension of $ K $. When $ s \geq 3 $, we find some examples in which statement (A) does not hold but statement (C) holds, which is a new phenomenon not appearing in the planar cases. Through a different probabilistic approach, we establish the equivalence of statements (A) and (B) for Bedford–McMullen sponges.

The global C0 linearization theorem on Banach spaces was first proposed by Pugh [26], but it requires that the nonlinear term is globally bounded. In the present paper, we discuss global linearization of semilinear autonomous ordinary differential equations on Banach spaces assuming that the linear part is hyperbolic (including contraction as a particular case) and that the nonlinear term is only Lipschitz with a sufficiently small Lipschitz constant. To overcome the difficulties arising in this problem, in this paper, we rely on a splitting lemma to decouple the hyperbolic system into a contractive system along the stable manifold and an expansive system along the unstable manifold. We then construct a transformation to linearize a contractive/expansive system, which is defined by the crossing time with respect to the unit sphere. To demonstrate the strength of our result, we apply our results to a nonlinear Duffing oscillator without external excitation.

We consider the Perron–Frobenius operator defined on the space of functions of bounded variation for the beta-map $\tau _\beta (x)=\beta x$ (mod $1$) for $\beta \in (1,\infty )$, and investigate its isolated eigenvalues except $1$, called non-leading eigenvalues in this paper. We show that the set of $\beta $ such that the corresponding Perron–Frobenius operator has at least one non-leading eigenvalue is open and dense in $(1,\infty )$. Furthermore, we establish the Hölder continuity of each non-leading eigenvalue as a function of $\beta $ and show in particular that it is continuous but non-differentiable, whose analogue was conjectured by Flatto, Lagarias and Poonen in [The zeta function of the beta transformation. Ergod. Th. & Dynam. Sys. 14 (1994), 237–266]. In addition, for an eigenfunctional of the Perron–Frobenius operator corresponding to an isolated eigenvalue, we give an explicit formula for the value of the functional applied to the indicator function of every interval. As its application, we provide three results related to non-leading eigenvalues, one of which states that an eigenfunctional corresponding to a non-leading eigenvalue cannot be expressed by any complex measure on the interval, which is in contrast to the case of the leading eigenvalue $1$.

Ergodic optimization aims to describe dynamically invariant probability measures that maximize the integral of a given function. For a wide class of intrinsically ergodic subshifts over a finite alphabet, we show that the space of continuous functions on the shift space contains two disjoint subsets: one is a dense $G_\delta $ set for which all maximizing measures have ‘relatively small’ entropy; the other is the set of functions having uncountably many, fully supported ergodic maximizing measures with ‘relatively large’ entropy. This result generalizes and unifies the results of Morris [Discrete Contin. Dyn. Syst. 27 (2010), 383–388] and Shinoda [Nonlinearity 31 (2018), 2192–2200] on symbolic dynamics, and applies to a wide class of intrinsically ergodic non-Markov symbolic dynamics without the Bowen specification property, including any transitive piecewise monotonic interval map, some coded shifts, and multidimensional $\beta $-transformations. Along with these examples of application, we provide an example of an intrinsically ergodic subshift with positive obstruction entropy to specification.

We consider local escape rates and hitting time statistics for unimodal interval maps of Misiurewicz–Thurston type. We prove that for any point z in the interval, there is a local escape rate and hitting time statistics that is one of three types. While it is key that we cover all points z, the particular interest here is when z is periodic and in the postcritical orbit that yields the third part of the trichotomy. We also prove generalized asymptotic escape rates of the form first shown by Bruin, Demers and Todd.

Using bi-contact geometry, we define a new type of Dehn surgery on an Anosov flow with orientable weak invariant foliations. The Anosovity of the new flow is strictly connected to contact geometry and the Reeb dynamics of the defining bi-contact structure. This approach gives new insights into the properties of the flows produced by Goodman surgery and clarifies under which conditions Goodman’s construction yields an Anosov flow. Our main application gives a necessary and sufficient condition to generate a contact Anosov flow by Foulon–Hasselblatt Legendrian surgery on a geodesic flow. In particular, we show that this is possible if and only if the surgery is performed along a simple closed geodesic. As a corollary, we have that any positive skewed $\mathbb {R}$-covered Anosov flow obtained by a single surgery on a closed orbit of a geodesic flow is orbit equivalent to a positive contact Anosov flow.