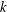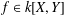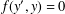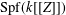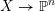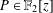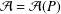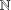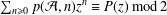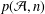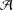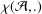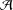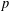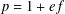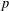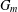Refine listing
Actions for selected content:
205 results in 12xxx
A general approach to the integral functionals of epidemic processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 593-609
- Print publication:
- June 2018
-
- Article
- Export citation
A NOTE ON THE FUNDAMENTAL THEOREM OF ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 382-385
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Existence of valuations with smallestnormalized volume
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 820-849
- Print publication:
- April 2018
-
- Article
- Export citation
TORSION OF ABELIAN VARIETIES OVER LARGE ALGEBRAIC EXTENSIONS OF
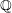 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 10 November 2017, pp. 46-86
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
AX–SCHANUEL CONDITION IN ARBITRARY CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1157-1213
- Print publication:
- November 2019
-
- Article
- Export citation
CM FIELDS WITHOUT UNIT-PRIMITIVE ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 20 September 2017, pp. 398-399
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Generalized Euler characteristic in power-bounded T-convex valued fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 14 September 2017, pp. 2591-2642
- Print publication:
- December 2017
-
- Article
- Export citation
Corrigendum: Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2658-2665
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
AN INFINITE FAMILY OF NINTH DEGREE DIHEDRAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 47-53
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
The
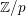 $\mathbb{Z}/p$ metabelian birational
$\mathbb{Z}/p$ metabelian birational 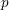 $p$ -adic section conjecture for varieties
$p$ -adic section conjecture for varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 04 May 2017, pp. 1433-1445
- Print publication:
- July 2017
-
- Article
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
A Generalization of the Eisenstein–Dumas–Schönemann Irreducibility Criterion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 937-945
-
- Article
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
DEFORMATIONS OF DIFFERENTIAL ARCS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 405-410
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
ALGORITHMS FOR GALOIS GROUP COMPUTATIONS OVER MULTIVARIATE FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 169-170
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Failures of weak approximation in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1435-1475
- Print publication:
- July 2016
-
- Article
- Export citation
SETS WITH EVEN PARTITION FUNCTIONS AND CYCLOTOMIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 289-302
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Relative Manin–Mumford for Semi-Abelian Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 18 January 2016, pp. 837-875
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 375-387
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
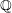
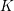
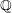
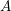
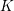
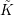
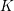
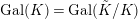
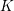
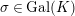
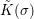

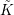
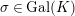
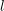
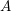
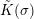
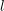

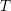
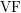
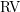
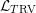
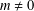
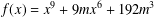
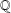
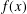
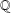
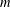
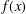
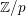
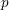
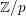
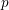
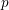
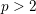
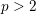
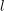


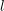
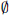 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.