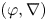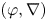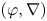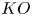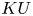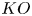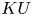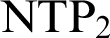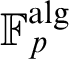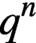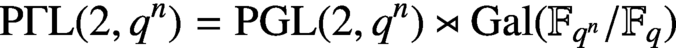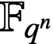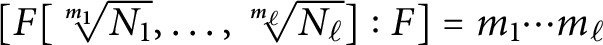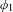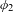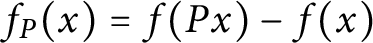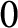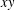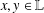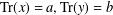Refine listing
Actions for selected content:
205 results in 12xxx
Logarithmic growth filtrations for
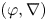 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1265-1301
- Print publication:
- June 2021
-
- Article
- Export citation
Brauer groups and Galois cohomology of commutative ring spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1211-1264
- Print publication:
- June 2021
-
- Article
- Export citation
Transfer Principles in Henselian Valued Fields
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 222-223
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
GENERATORS OF FINITE FIELDS WITH PRESCRIBED TRACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 355-366
- Print publication:
- June 2022
-
- Article
- Export citation
A CLASS OF FIELDS WITH A RESTRICTED MODEL COMPLETENESS PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 701-708
- Print publication:
- June 2021
-
- Article
- Export citation
STRICTLY REAL FUNDAMENTAL THEOREM OF ALGEBRA USING POLYNOMIAL INTERLACING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 249-255
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
MÖBIUS–FROBENIUS MAPS ON IRREDUCIBLE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 66-77
- Print publication:
- August 2021
-
- Article
- Export citation
On the degree of repeated radical extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 877-885
- Print publication:
- December 2021
-
- Article
- Export citation
ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 428-437
- Print publication:
- June 2021
-
- Article
- Export citation
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
DIMENSIONAL GROUPS AND FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 918-936
- Print publication:
- September 2020
-
- Article
- Export citation
INVARIANT HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 713-739
- Print publication:
- March 2022
-
- Article
- Export citation
Criteria for periodicity and an application to elliptic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 530-540
- Print publication:
- September 2021
-
- Article
- Export citation
A NOTE ON p-ADIC SIMPLICIAL VOLUMES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 563-583
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation
EQUATIONAL THEORIES OF FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 828-851
- Print publication:
- June 2020
-
- Article
- Export citation
ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 14 May 2020, pp. 264-288
- Print publication:
- April 2022
-
- Article
- Export citation
PRIMITIVE RECURSIVE DECIDABILITY FOR THE RING OF INTEGERS OF THE COMPOSITUM OF ALL SYMMETRIC EXTENSIONS OF ℚ
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 291-296
- Print publication:
- May 2021
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
APPLICATIONS OF SYSTEMS OF QUADRATIC FORMS TO GENERALISED QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 374-386
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation