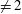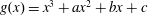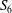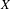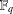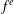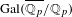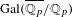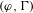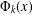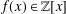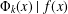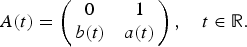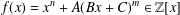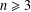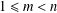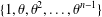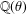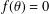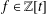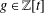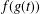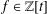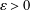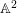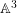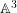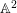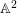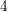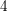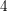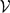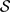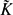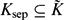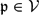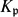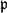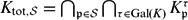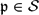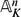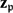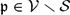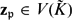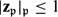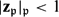Refine listing
Actions for selected content:
205 results in 12xxx
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
Galois Groups of Even Sextic Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 670-676
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
DEFINABLE SETS OF BERKOVICH CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1275-1339
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
A NEW PROOF OF THE CARLITZ–LUTZ THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 56-60
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
PERMUTATION POLYNOMIALS OF DEGREE 8 OVER FINITE FIELDS OF ODD CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 40-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Fraud risk assessment within blockchain transactions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 443-467
- Print publication:
- June 2019
-
- Article
- Export citation
COHOMOLOGY AND OVERCONVERGENCE FOR REPRESENTATIONS OF POWERS OF GALOIS GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 11 April 2019, pp. 361-421
- Print publication:
- March 2021
-
- Article
- Export citation
CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 41-47
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Hyers–Ulam stability for equations with differences and differential equations with time-dependent and periodic coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 20 March 2019, pp. 2175-2188
- Print publication:
- October 2020
-
- Article
- Export citation
A BRIEF NOTE ON SOME INFINITE FAMILIES OF MONOGENIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 239-244
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
SMOOTH VALUES OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 245-261
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
- Print publication:
- 2019
-
- Article
- Export citation
ON SEPARABLE
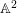 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 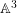 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 346-354
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
EXTENSIONS OF HILBERTIAN RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1-11
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
COORDINATISING PLANES OF PRIME POWER ORDER USING FINITE FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 184-199
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On the Integral Degree of Integral Ring Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 25-46
-
- Article
- Export citation
Four-fold Massey products in Galois cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 1921-1959
- Print publication:
- September 2018
-
- Article
- Export citation
CONTINUITY OF ROOTS, REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 448-455
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Bounding the Number of Common Zeros of Multivariate Polynomials and Their Consecutive Derivatives
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 August 2018, pp. 253-279
-
- Article
- Export citation
STRONG APPROXIMATION THEOREM FOR ABSOLUTELY IRREDUCIBLE VARIETIES OVER THE COMPOSITUM OF ALL SYMMETRIC EXTENSIONS OF A GLOBAL FIELD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 373-380
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation