Let K be a complete discrete valuation field of mixed characteristic (0,p), with possibly imperfect residue field. We prove a Hasse–Arf theorem for the arithmetic ramification filtrations on GK, except possibly in the absolutely unramified and non-logarithmic case, or the p=2 and logarithmic case. As an application, we obtain a Hasse–Arf theorem for filtrations on finite flat group schemes over 𝒪K.

Let Fq be a finite field with q elements, V an n-dimensional vector space over Fq and 𝒱 the projective space associated to V. Let G≤GLn(Fq) be a classical group and PG be the corresponding projective group. In this note we prove that if Fq (V )G is purely transcendental over Fq with homogeneous polynomial generators, then Fq (𝒱)PG is also purely transcendental over Fq. We compute explicitly the generators of Fq (𝒱)PG when G is the symplectic, unitary or orthogonal group.

We refine a result of Dubickas on the maximal multiplicity of the roots of a complex polynomial, and obtain several separability criteria for complex polynomials with large leading coefficient. We also give p-adic analogous results for polynomials with integer coefficients.

We consider valued fields with a value-preserving automorphism and improve on model-theoretic results by Bélair, Macintyre and Scanlon on these objects by dropping assumptions on the residue difference field. In the equicharacteristic 0 case we describe the induced structure on the value group and the residue difference field.

Let E/k be a function field over an infinite field of constants. Assume that E/k(x) is a separable extension of degree greater than one such that there exists a place of degree one of k(x) ramified in E. Let K/k be a function field. We prove that there exist infinitely many nonisomorphic separable extensions L/K such that [L:K]=[E:k(x)] and AutkL=AutKL≅Autk(x)E.

Let K be a complete ultrametric algebraically closed field and let A be the Banach K-algebra of bounded analytic functions in the ‘open’ unit disc D of K provided with the Gauss norm. Let Mult(A,‖ · ‖) be the set of continuous multiplicative semi-norms of A provided with the topology of simple convergence, let Multm(A, ‖ · ‖) be the subset of the φ ∈ Mult(A, ‖ · ‖) whose kernel is a maximal ideal and let Multa(A, ‖ · ‖) be the subset of the φ ∈ Mult(A, ‖ · ‖) whose kernel is a maximal ideal of the form (x − a)A with a ∈ D. We complete the characterization of continuous multiplicative norms of A by proving that the Gauss norm defined on polynomials has a unique continuation to A as a norm: the Gauss norm again. But we find prime closed ideals that are neither maximal nor null. The Corona Problem on A lies in two questions: is Multa(A, ‖ · ‖) dense in Multm(A, ‖ · ‖)? Is it dense in Multm(A, ‖ · ‖)? In a previous paper, Mainetti and Escassut showed that if each maximal ideal of A is the kernel of a unique φ ∈ Mult(m(A, ‖ · ‖), then the answer to the first question is affirmative. In particular, the authors showed that when K is strongly valued each maximal ideal of A is the kernel of a unique φ ∈ Mult(m(A, ‖ · ‖). Here we prove that this uniqueness also holds when K is spherically complete, and therefore so does the density of Multa(A, ‖ · ‖) in Multm(A, ‖ · ‖).

In this article we introduce and prove a ℤ/p meta-abelian form of the birationalp-adic section conjecture for curves. This is a much stronger result than the usual p-adic birational section conjecture for curves, and makes an effective p-adic section conjecture for curves quite plausible.

The notion of a prolongation of an algebraic variety is developed in an abstract setting that generalizes the difference and (Hasse) differential contexts. An interpolating map that compares these prolongation spaces with algebraic jet spaces is introduced and studied.

A theorem of Kuyk says that every Abelian extension of a Hilbertian field is Hilbertian. We conjecture that for an Abelian variety A defined over a Hilbertian field K every extension L of K in K(Ator) is Hilbertian. We prove our conjecture when K is a number field. The proof applies a result of Serre about l-torsion of Abelian varieties, information about l-adic analytic groups, and Haran's diamond theorem.

Let υ be a valuation on K with value group Gυ, residue field kυ, rank υ = t and K (x1, …, xn) be the field of rational functions over K with n variables. If G is the direct sum of G1 and d infinite cyclic groups where G1 is a totally ordered group containing Gυ as an ordered subgroup with [G1 : Gυ] < ∞ and k′ is a finite field extension of kυ then there exists a residual transcendental extension u of υ to K (x1, …, xn) such that rank u = t + d, Gu = G the algebraic closure of kυ in kυ is k′ and trans deg ku/kυ = n − d.

We study the asymptotical behaviour of the moduli space of morphisms of given anticanonical degree from a rational curve to a split toric variety, when the degree goes to infinity. We obtain in this case a geometric analogue of Manin’s conjecture about rational points of bounded height on varieties defined over a global field. The study is led through a generating series whose coefficients lie in a Grothendieck ring of motives, the motivic height zeta function. In order to establish convergence properties of this function, we use a notion of motivic Euler product. It relies on a construction of Denef and Loeser which associates a virtual motive to a first order logic ring formula.

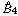We study behaviours of the ‘equianharmonic’ parameter of the Grothendieck–Teichmüller group introduced by Lochak and Schneps. Using geometric construction of a certain one-parameter family of quartics, we realize the Galois action on the fundamental group of a punctured Mordell elliptic curve in the standard Galois action on a specific subgroup of the braid group . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.

We prove that n-hypergraphs can be interpreted in e-free perfect PAC fields in particular in pseudofinite fields. We use methods of function field arithmetic, more precisely we construct generic polynomials with alternating groups as Galois groups over a function field.

For a ∇-module M over the ring K[[x]]0 of bounded functions over a p-adic local field K we define the notion of special and generic log-growth filtrations on the base of the power series development of the solutions and horizontal sections. Moreover, if M also admits a Frobenius structure then it is endowed with generic and special Frobenius slope filtrations. We will show that in the case of M a ϕ–∇-module of rank 2, the Frobenius polygon for M and the log-growth polygon for its dual, Mv, coincide, this is proved by showing explicit relationships between the filtrations. This will lead us to formulate some conjectural links between the behaviours of the filtrations arising from the log-growth and Frobenius structures of the differential module. This coincidence between the two polygons was only known for the hypergeometric cases by Dwork.

Natural sufficient conditions for a polynomial to have a local minimum at a point are considered. These conditions tend to hold with probability 1. It is shown that polynomials satisfying these conditions at each minimum point have nice presentations in terms of sums of squares. Applications are given to optimization on a compact set and also to global optimization. In many cases, there are degree bounds for such presentations. These bounds are of theoretical interest, but they appear to be too large to be of much practical use at present. In the final section, other more concrete degree bounds are obtained which ensure at least that the feasible set of solutions is not empty.

We draw a connection between the model-theoretic notions of modularity (or one-basedness), orthogonality and internality, as applied to difference fields, and questions of descent in in algebraic dynamics. In particular we prove in any dimension a strong dynamical version of Northcott's theorem for function fields, answering a question of Szpiro and Tucker and generalizing a theorem of Baker's for the projective line.

The paper comes in three parts. This first part contains an exposition some of the main results of the model theory of difference fields, and their immediate connection to questions of descent in algebraic dynamics. We present the model-theoretic notion of internality in a context that does not require a universal domain with quantifier-elimination. We also note a version of canonical heights that applies well beyond polarized algebraic dynamics. Part II sharpens the structure theory to arbitrary base fields and constructible maps where in part I we emphasize finite base change and correspondences. Part III will include precise structure theorems related to the Galois theory considered here, and will enable a sharpening of the descent results for non-modular dynamics.

This second part of the paper strengthens the descent theory described in the first part torational maps and arbitrary base fields. We obtain in particular a decomposition of any difference field extension into a tower of finite, field-internal and one-based difference field extensions. This is needed in order to obtain the ‘dynamical Northcott’ Theorem 1.11 of Part I in sharp form.

Dichotomies in various conjectures from algebraic geometry are in fact occurrences of the dichotomy among Zariski structures. This is what Hrushovski showed and which enabled him to solve, positively, the geometric Mordell–Lang conjecture in positive characteristic. Are we able now to avoid this use of Zariski structures? Pillay and Ziegler have given a direct proof that works for semi-abelian varieties they called ‘very thin’, which include the ordinary abelian varieties. But it does not apply in all generality: we describe here an abelian variety which is not very thin. More generally, we consider from a model-theoretical point of view several questions about the fields of definition of semi-abelian varieties.

Let k be an algebraically closed field of positive characteristic p. We consider which finite groups G have the property that every faithful action of G on a connected smooth projective curve over k lifts to characteristic zero. Oort conjectured that cyclic groups have this property. We show that if a cyclic-by-p group G has this property, then G must be either cyclic or dihedral, with the exception of A4 in characteristic two. This proves one direction of a strong form of the Oort conjecture.

We develop the theory of p-adic confluence of q-difference equations. The main result is the fact that, in the p-adic framework, a function is a (Taylor) solution of a differential equation if and only if it is a solution of a q-difference equation. This fact implies an equivalence, called confluence, between the category of differential equations and those of q-difference equations. We develop this theory by introducing a category of sheaves on the disk D−(1,1), for which the stalk at 1 is a differential equation, the stalk at q isa q-difference equation if q is not a root of unity, and the stalk at a root of unity ξ is a mixed object, formed by a differential equation and an action of σξ.