Refine listing
Actions for selected content:
205 results in 12xxx
A DEFINABLE
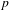 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
SOME PROPERTIES OF ANALYTIC DIFFERENCE VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 29 May 2015, pp. 447-499
- Print publication:
- June 2017
-
- Article
- Export citation
Bespoke finite difference schemes that preserve multiple conservation laws
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 May 2015, pp. 372-403
-
- Article
-
- You have access
- Export citation
DIFFERENCE ALGEBRAIC RELATIONS AMONG SOLUTIONS OF LINEAR DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 17 April 2015, pp. 59-119
- Print publication:
- February 2017
-
- Article
- Export citation
Projective geometry in characteristic one and the epicyclic category
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 95-132
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 1096-1156
- Print publication:
- June 2015
-
- Article
- Export citation
ALGEBRAIC INDEPENDENCE OF CERTAIN MAHLER FUNCTIONS AND OF THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 289-310
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Rational rigidity for
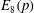 ${E}_{8}(p)$
${E}_{8}(p)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1679-1702
- Print publication:
- October 2014
-
- Article
- Export citation
ON THE SUBSTITUTION THEOREM FOR RINGS OF SEMIALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 01 July 2014, pp. 857-894
- Print publication:
- October 2015
-
- Article
- Export citation
A NOTE ON INTERPOLATION OF PERMUTATIONS OF A SUBSET OF A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 213-219
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
CONSTRUCTING PERMUTATION POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 420-430
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Unipotent differential algebraic groups as parameterized differential Galois groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 671-700
- Print publication:
- October 2014
-
- Article
- Export citation
Rationality problems and conjectures of Milnor and Bloch–Kato
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1312-1326
- Print publication:
- August 2013
-
- Article
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
ON PERMUTATION BINOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 March 2013, pp. 112-124
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
CONSTRUCTIONS BY RULER AND COMPASS, TOGETHER WITH A FIXED CONIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 473-478
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Orderings and signatures of higher level on multirings and hyperfields
- Part of
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 May 2012, pp. 489-518
- Print publication:
- December 2012
-
- Article
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Hilbertianity of fields of power series
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 351-361
- Print publication:
- April 2012
-
- Article
- Export citation
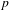
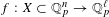
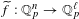
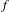
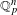
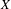
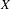


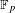
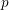
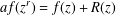


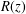
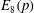
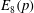
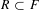
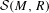
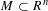
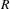
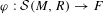
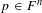
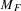
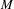
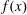
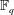

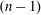


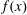

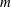
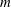

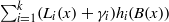
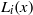
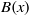
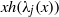
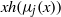
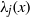
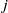
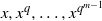
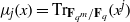
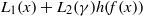
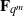
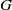
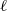
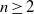

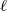
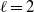

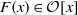

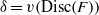
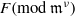

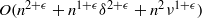
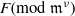
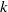
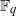
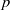
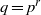
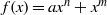
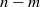
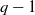
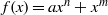
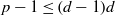
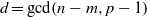
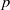
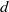
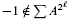 to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.
to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.