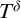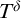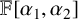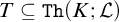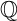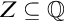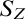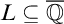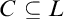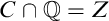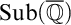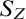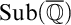Refine listing
Actions for selected content:
205 results in 12xxx
On ordinary differentially large fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RINGS WITH COMMON DIVISION, COMMON MEADOWS AND THEIR CONDITIONAL EQUATIONAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-31
-
- Article
- Export citation
DEFINABLE HENSELIAN VALUATIONS IN POSITIVE RESIDUE CHARACTERISTIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE-DIMENSIONAL DIFFERENTIAL-ALGEBRAIC PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 603-626
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometry of tropical extensions of hyperfields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERIC DERIVATIONS ON ALGEBRAICALLY BOUNDED STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-27
-
- Article
- Export citation
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 490-496
- Print publication:
- June 2025
-
- Article
- Export citation
ARTIN–SCHREIER EXTENSIONS AND COMBINATORIAL COMPLEXITY IN HENSELIAN VALUED FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1747-1767
- Print publication:
- December 2024
-
- Article
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
- Export citation
MORE ON GALOIS COHOMOLOGY, DEFINABILITY, AND DIFFERENTIAL ALGEBRAIC GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 496-515
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Undecidability of polynomial inequalities in weighted graph homomorphism densities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian absolute Galois groups: In Erinnerung an Wulf-Dieter Geyer (1939–2019)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. 359-367
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On definable groups and D-groups in certain fields with a generic derivation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 15 January 2024, pp. 459-480
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO EXAMPLES CONCERNING EXISTENTIAL UNDECIDABILITY IN FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 November 2023, pp. 552-563
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
AN ALGEBRAIC INTERPRETATION OF THE SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 498-506
- Print publication:
- June 2024
-
- Article
- Export citation
PAC STRUCTURES AS INVARIANTS OF FINITE GROUP ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1340-1375
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE UNDECIDABILITY IN NIP FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 04 October 2023, pp. 509-532
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TOPOLOGICAL APPROACH TO UNDEFINABILITY IN ALGEBRAIC EXTENSIONS OF
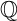 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 September 2023, pp. 626-655
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation