Refine listing
Actions for selected content:
99 results in 46Axx
BARRELLED SPACES WITH(OUT) SEPARABLE QUOTIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 295-303
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
HYPERGROUP ALGEBRAS AS TOPOLOGICAL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 486-493
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
BORNOLOGIES AND LOCALLY LIPSCHITZ FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 257-263
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
THE SIMILARITY DEGREE OF SOME
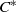 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 June 2013, pp. 60-69
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
THE STRONG DUAL OF MEASURE ALGEBRAS WITH CERTAIN LOCALLY CONVEX TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 08 April 2013, pp. 353-365
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
NOTE ABOUT LINDELÖF Σ-SPACES υX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 28 September 2011, pp. 114-120
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
STRICT TOPOLOGY AS A MIXED TOPOLOGY ON LEBESGUE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 504-515
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
THE STRICT TOPOLOGY ON THE DISCRETE LEBESGUE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 241-255
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
NONEXPANSIVE MAPPINGS AND EXPANSIVE MAPPINGS ON THE UNIT SPHERES OF SOME F-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 April 2010, pp. 22-30
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
NONCOMPLETE MACKEY TOPOLOGIES ON BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 March 2010, pp. 409-413
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
THE FATOU COMPLETION OF A FRÉCHET FUNCTION SPACE AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 08 December 2009, pp. 49-60
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
WHEN LATTICE HOMOMORPHISMS OF ARCHIMEDEAN VECTOR LATTICES ARE RIESZ HOMOMORPHISMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 263-273
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
NONEXPANSIVE MAPPINGS ON THE UNIT SPHERES OF SOME BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 139-146
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
THE DIRICHLET PROBLEM FOR BAIRE-TWO FUNCTIONS ON SIMPLICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 285-297
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A WEAKLY ANALYTIC LOCALLY CONVEX SPACE WHICH IS NOT K-ANALYTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 31-35
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
An Open Mapping Theorem For Pro-Lie Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-78
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Spaces of vector functions that are integrable with respect to vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-109
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Topologies on spaces of vector-valued meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-290
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
Invariants in abstract mapping pairs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-382
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
The Exponential Representation of Holomorphic Functions of Uniformly Bounded Type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-246
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
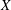
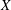
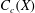
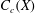
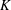
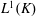
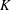
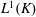
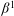
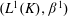
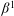
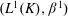
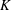
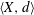
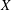
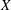
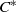
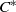
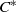
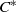
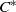
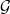

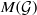
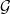
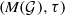
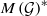
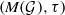
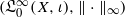 . Next, by showing that
. Next, by showing that 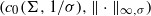 . We also show that, except for the case where Σ is finite, there are infinitely many such locally convex topologies on
. We also show that, except for the case where Σ is finite, there are infinitely many such locally convex topologies on 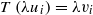 for each
for each 