Refine listing
Actions for selected content:
99 results in 46Axx
Positive semigroups of operators on Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-94
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Quasi-suprabarrelled spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-145
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
On homomorphisms of an orthogonally decomposable Hilbert space, III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-295
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
Monotonic norms in ordered Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-219
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
On Homomorphisms of an Orthogonally Decomposable Hilbert Space II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-163
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
An Inequality Implicit Function Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-150
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
A non-absolutely summing operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 70-73
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Extension of Riesz homomorphisms. III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-46
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
On extremal points of the unit ball in the Banach space of Lipschitz continuous functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-98
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Relatively central operators on Archimedean vector lattices II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-298
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Semicontinuity of multifunctions connected with optimization with respect to cones
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-193
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
The range of an o-weakly compact mapping
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-399
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Extension of Riesz homomorphisms.I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 107-120
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Orthomorphisms of a commutative W*-algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-168
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Extension and inversion of extended orthomorphisms on Riesz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-242
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Calculus in f-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 110-116
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Continuity properties of vector-valued convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 404-415
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
Sur les mesures coniques localisables
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 394-400
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
A decomposition theorem in tensor products of Archimedean vector lattices
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 302-305
- Print publication:
- December 1979
-
- Article
- Export citation
 –semigroups is also given.
–semigroups is also given.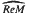 of densely defined self-adjoint transformations affiliated with
of densely defined self-adjoint transformations affiliated with  ∈ Orth
∈ Orth