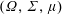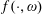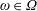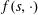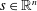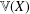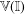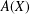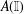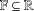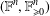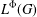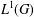Refine listing
Actions for selected content:
99 results in 46Axx
Completeness of Infinite-dimensional Lie Groups in Their Left Uniformity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-152
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
Krivine’s Function Calculus and Bochner Integration
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 663-669
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
The Fréchet Schwartz Algebra of Uniformly Convergent Dirichlet Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 933-942
-
- Article
- Export citation
Conjugate duality in stochastic controls with delay
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1011-1036
- Print publication:
- December 2017
-
- Article
- Export citation
Homotopy linear algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 293-325
- Print publication:
- April 2018
-
- Article
- Export citation
SUBSPACES OF THE FREE TOPOLOGICAL VECTOR SPACE ON THE UNIT INTERVAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 August 2017, pp. 110-118
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
A Convenient Notion of Compact Set for Generalized Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 03 April 2017, pp. 57-92
-
- Article
- Export citation
ON MULTIPLIERS BETWEEN SOME SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 146-153
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
COMPATIBLE LOCALLY CONVEX TOPOLOGIES ON NORMED SPACES: CARDINALITY ASPECTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 139-145
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
‘POSITIVELY HOMOGENEOUS LATTICE HOMOMORPHISMS BETWEEN RIESZ SPACES NEED NOT BE LINEAR’
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 444-445
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
METRIC REGULARITY—A SURVEY PART II. APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 376-417
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
THE CESÀRO OPERATOR IN THE FRÉCHET SPACES ℓp+ AND L p−
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 273-287
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
FINITE-DIMENSIONAL ORDERED VECTOR SPACES WITH RIESZ INTERPOLATION AND EFFROS–SHEN’S UNIMODULARITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 277-287
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
AN OPEN MAPPING THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 65-69
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
The Growth Bound for Strongly Continuous Semigroups on Fréchet Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 23 November 2015, pp. 801-810
-
- Article
- Export citation
CLASSES OF SEQUENTIALLY LIMITED OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 573-586
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
ON A QUESTION OF BOURAS CONCERNING WEAK COMPACTNESS OF ALMOST DUNFORD–PETTIS SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 111-114
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
SEPARATION OF CONVEX SETS IN EXTENDED NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 145-165
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
A CONVOLUTION-INDUCED TOPOLOGY ON THE ORLICZ SPACE OF A LOCALLY COMPACT GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 19 January 2015, pp. 1-11
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Krein-Smulian-Type Theorems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 441-444
-
- Article
-
- You have access
- Export citation