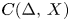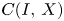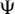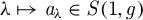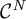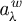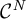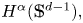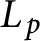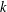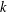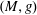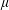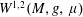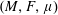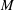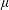Refine listing
Actions for selected content:
220 results in 46Exx
An example regarding Kalton's paper ‘isomorphisms between spaces of vector-valued continuous functions’
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 615-619
-
- Article
- Export citation
EMBEDDING THEOREM OF THE WEIGHTED SOBOLEV–LORENTZ SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 358-375
-
- Article
- Export citation
Quasi-equivalence of bases in some Whitney spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-115
- Print publication:
- March 2022
-
- Article
- Export citation
NORMAL FUNCTIONALS ON LIPSCHITZ SPACES ARE WEAK* CONTINUOUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2093-2102
- Print publication:
- November 2022
-
- Article
- Export citation
EQUIVALENCE OF ELLIPTICITY AND THE FREDHOLM PROPERTY IN THE WEYL-HÖRMANDER CALCULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1363-1389
- Print publication:
- July 2022
-
- Article
- Export citation
WEIGHTED COMPOSITION OPERATORS BETWEEN LORENTZ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 493-505
- Print publication:
- June 2021
-
- Article
- Export citation
Optimal approximants and orthogonal polynomials in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 November 2020, pp. 428-456
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
The Fourier extension operator of distributions in Sobolev spaces of the sphere and the Helmholtz equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 1768-1789
- Print publication:
- December 2021
-
- Article
- Export citation
Sharp affine Trudinger–Moser inequalities: A new argument
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 October 2020, pp. 765-778
- Print publication:
- December 2021
-
- Article
- Export citation
Continuity of solutions for the Δϕ-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 1355-1382
- Print publication:
- August 2021
-
- Article
- Export citation
On a family of torsional creep problems in Finsler metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 02 September 2020, pp. 24-41
- Print publication:
- February 2022
-
- Article
- Export citation
ON THE STABILITY OF THE DIFFERENTIAL PROCESS GENERATED BY COMPLEX INTERPOLATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 303-334
- Print publication:
- January 2022
-
- Article
- Export citation
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 June 2020, pp. 869-920
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
On Trudinger-type Inequalities in Orlicz-Morrey Spaces of an Integral Form
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 03 April 2020, pp. 75-90
- Print publication:
- March 2021
-
- Article
- Export citation
The spectrum of the mean curvature operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 451-463
- Print publication:
- April 2021
-
- Article
- Export citation
Embeddings of homogeneous Sobolev spaces on the entire space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 296-328
- Print publication:
- February 2021
-
- Article
- Export citation
ON A PROBLEM OF TALAGRAND CONCERNING SEPARATELY CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 06 February 2020, pp. 1719-1728
- Print publication:
- September 2021
-
- Article
- Export citation
THE DISTRIBUTIONAL
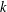 $k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES
$k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 496-507
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
SOBOLEV’S INEQUALITY FOR MUSIELAK–ORLICZ–MORREY SPACES OVER METRIC MEASURE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 02 October 2019, pp. 371-385
-
- Article
- Export citation
Infinitesimal Hilbertianity of Weighted Riemannian Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 118-140
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation