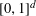Refine listing
Actions for selected content:
220 results in 46Exx
Pointwise Characterizations of Even Order Sobolev Spaces via Derivatives of Ball Averages
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 681-699
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Exponential models by Orlicz spaces and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 682-700
- Print publication:
- September 2018
-
- Article
- Export citation
Solving the Equation
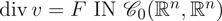 $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
$\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1055-1061
-
- Article
- Export citation
Sobolev Algebras Through a ‘Carré Du Champ’ Identity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1041-1054
-
- Article
- Export citation
Littlewood–Paley characterizations of fractional Sobolev spaces via averages on balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 1135-1163
- Print publication:
- December 2018
-
- Article
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
-
- Article
-
- You have access
- Export citation
Weak-Type Boundedness of the Fourier Transform on Rearrangement Invariant Function Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 879-890
-
- Article
- Export citation
A weighted weak-type bound for Haar multipliers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 643-658
- Print publication:
- June 2018
-
- Article
- Export citation
Poincaré inequalities for Sobolev spaces with matrix-valued weights and applications to degenerate partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 April 2018, pp. 61-100
- Print publication:
- February 2019
-
- Article
- Export citation
An Inductive Julia-Carathéodory Theorem for Pick Functions in Two Variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 647-660
-
- Article
- Export citation
LITTLEWOOD–PALEY CHARACTERIZATIONSOF ANISOTROPIC WEAK MUSIELAK–ORLICZHARDY SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 16 March 2018, pp. 39-78
-
- Article
-
- You have access
- HTML
- Export citation
AN EXTENSION OF THE BANACH–STONE THEOREM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1-23
-
- Article
-
- You have access
- Export citation
THE BOUNDED APPROXIMATION PROPERTY FOR THE WEIGHTED SPACES OF HOLOMORPHIC MAPPINGS ON BANACH SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 07 September 2017, pp. 307-320
-
- Article
-
- You have access
- Export citation
Infinitely many solutions for equations of p(x)-Laplace type with the nonlinear Neumann boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 August 2017, pp. 1-31
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
From Hankel Operators to Carleson Measures in a Quaternionic Variable
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 17 July 2017, pp. 565-585
-
- Article
- Export citation
The algebra of symmetric analytic functions on L ∞
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 743-761
- Print publication:
- August 2017
-
- Article
- Export citation
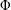 $\unicode[STIX]{x1D6F7}$ -CARLESON MEASURES AND MULTIPLIERS BETWEEN BERGMAN–ORLICZ SPACES OF THE UNIT BALL OF
$\unicode[STIX]{x1D6F7}$ -CARLESON MEASURES AND MULTIPLIERS BETWEEN BERGMAN–ORLICZ SPACES OF THE UNIT BALL OF 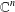 $\mathbb{C}^{n}$
$\mathbb{C}^{n}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 March 2017, pp. 63-79
-
- Article
-
- You have access
- Export citation
Iterating Bilinear Hardy Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 955-971
-
- Article
- Export citation
On the Global Gaussian Lipschitz Space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 03 January 2017, pp. 707-720
-
- Article
- Export citation
DISCREPANCY OF SECOND ORDER DIGITAL SEQUENCES IN FUNCTION SPACES WITH DOMINATING MIXED SMOOTHNESS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 863-894
- Print publication:
- 2017
-
- Article
- Export citation
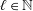
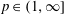
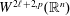
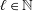
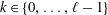
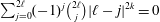
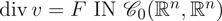
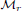 is the
is the 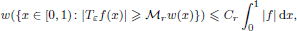
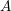
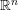
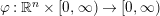
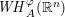
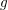
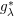

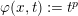
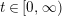
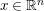
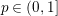
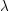
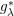
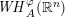
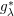
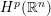
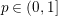
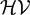
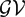
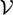
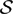
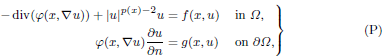
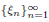 such that
such that 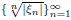 is bounded and turns to be separable. All this follows from our main result that the subalgebra of
is bounded and turns to be separable. All this follows from our main result that the subalgebra of 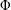
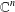
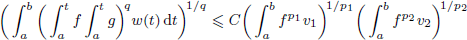
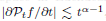 , where
, where 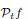 is the Poisson integral of the function
is the Poisson integral of the function