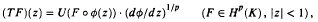Refine listing
Actions for selected content:
222 results in 46Exx
Semicontinuous functions and convex sets in C(K) spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-121
-
- Article
-
- You have access
- Export citation
Maximal ideal space of function algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-90
-
- Article
-
- You have access
- Export citation
Composition operators in Orlicz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-206
-
- Article
-
- You have access
- Export citation
The isometries of Hp(K)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-33
-
- Article
-
- You have access
- Export citation
Derivative-free characterizations of Qk spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 283-295
-
- Article
-
- You have access
- Export citation
On weighted inductive limits of spaces of Fréchet-valued continuous functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-242
-
- Article
-
- You have access
- Export citation
Multidimensional Hausdorff operators on the real Hardy space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
-
- Article
-
- You have access
- Export citation
The Schur and (weak) Dunford-Pettis properties in Banach lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-278
-
- Article
-
- You have access
- Export citation
Topologies on spaces of vector-valued meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-290
-
- Article
-
- You have access
- Export citation
Multidimensional Volterra integral equations of convolution type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 3 / May 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-312
-
- Article
-
- You have access
- Export citation
Composition operators on Qp spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-188
-
- Article
-
- You have access
- Export citation
Hilbert transform associated with finite maximal subdiagonal algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 388-404
-
- Article
-
- You have access
- Export citation
INVERSE IMAGES OF SECTORS BY FUNCTIONS IN WEIGHTED BERGMAN–ORLICZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 233-247
-
- Article
-
- You have access
- Export citation
Composition operators on μ-Bloch spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-75
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
Angelicity and the boundary problem
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-112
- Print publication:
- June 1998
-
- Article
- Export citation
On metrizable E with Cp(E) ≇ Cp(E) × Cp(E)
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-55
- Print publication:
- June 1995
-
- Article
- Export citation
On Baire-1/4 functions and spreading models
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-265
- Print publication:
- December 1994
-
- Article
- Export citation
Topological games and optimization problems
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-132
- Print publication:
- June 1994
-
- Article
- Export citation
On the space of continuous functions on a dyadic set
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-49
- Print publication:
- June 1991
-
- Article
- Export citation
Topological spaces with dense subspaces that are homeomorphic to complete metric spaces and the classification of C(K) Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-107
- Print publication:
- June 1987
-
- Article
- Export citation