Refine listing
Actions for selected content:
220 results in 46Exx
The Exponential Representation of Holomorphic Functions of Uniformly Bounded Type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-246
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Composition operators in Orlicz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-206
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Computation of nonsquare constants of Orlicz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-162
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Extreme Point Methods and Banach-Stone Theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-143
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Embeddings of ℓp into Non-commutative Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-350
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
The Schur and (weak) Dunford-Pettis properties in Banach lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-278
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Strongly omnipresent operators: general conditions and applications to composition operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Diameter-preserving linear bijections of function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 323-336
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Composition operators on Qp spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-188
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Weighted composition operators in weighted Banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-60
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
The domain space of an analytic composition operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-65
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Hilbert transform associated with finite maximal subdiagonal algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 388-404
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Angelicity and the boundary problem
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-112
- Print publication:
- June 1998
-
- Article
- Export citation
Composition operators between weighted Banach spaces of analytic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 101-118
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Maximal ideal space of function algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-90
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Isometries of Hilbert space valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 150-161
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
The uniform Kadec-Klee property for the Lorentz spaces Lw,1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-17
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
The locally convex topology on the space of meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-303
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
On the uniform Kadec-Klee property with respect to convergence in measure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-352
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
On metrizable E with Cp(E) ≇ Cp(E) × Cp(E)
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-55
- Print publication:
- June 1995
-
- Article
- Export citation
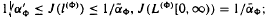 (ii) if φ (
(ii) if φ (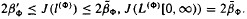
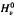 and
and 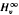 . we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces
. we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces 