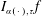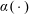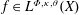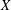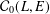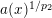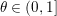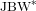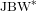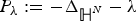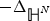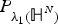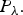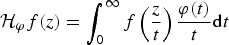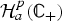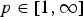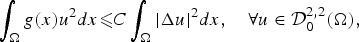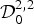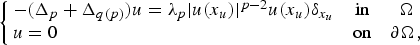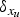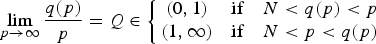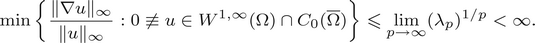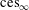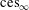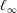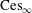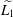Refine listing
Actions for selected content:
220 results in 46Exx
Sobolev’s Inequality for Riesz Potentials of Functions in Musielak–Orlicz–Morrey Spaces Over Non-doubling Metric Measure Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 06 September 2019, pp. 287-303
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
M-embedded symmetric operator spaces and the derivation problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 20 August 2019, pp. 607-622
- Print publication:
- November 2020
-
- Article
- Export citation
Two boundedness criteria for a class of operators on Musielak–Orlicz Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 13-35
-
- Article
- Export citation
ON A FUNCTION MODULE WITH APPROXIMATE HYPERPLANE SERIES PROPERTY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 341-348
-
- Article
-
- You have access
- Export citation
Orlicz–Besov Extension and Imbedding
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 01 July 2019, pp. 222-241
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
HERZ–MORREY SPACES ON THE UNIT BALL WITH VARIABLE EXPONENT APPROACHING
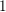 $1$ AND DOUBLE PHASE FUNCTIONALS
$1$ AND DOUBLE PHASE FUNCTIONALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1-34
-
- Article
- Export citation
ON THE EXTENSION OF ISOMETRIES BETWEEN THE UNIT SPHERES OF A
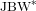 $\text{JBW}^{\ast }$-TRIPLE AND A BANACH SPACE
$\text{JBW}^{\ast }$-TRIPLE AND A BANACH SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 April 2019, pp. 277-303
- Print publication:
- January 2021
-
- Article
- Export citation
Bilinear forms on potential spaces in the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 19 March 2019, pp. 2117-2154
- Print publication:
- August 2020
-
- Article
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
An optimal improvement for the Hardy inequality on the hyperbolic space and related manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1699-1736
- Print publication:
- August 2020
-
- Article
- Export citation
Hausdorff operators on holomorphic Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1095-1112
- Print publication:
- June 2020
-
- Article
- Export citation
On the generalized Hardy-Rellich inequalities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 897-919
- Print publication:
- April 2020
-
- Article
- Export citation
Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1493-1522
- Print publication:
- December 2019
-
- Article
- Export citation
Isomorphic Structure of Cesàro and Tandori Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 501-532
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Solutions to the Schrödinger Equation on Manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 983-995
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Residually many BV homeomorphisms map a null set onto a set of full measure
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1047-1059
- Print publication:
- August 2019
-
- Article
- Export citation
General sharp weighted Caffarelli–Kohn–Nirenberg inequalities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 691-718
- Print publication:
- June 2019
-
- Article
- Export citation
The Spectra of Algebras of Group-Symmetric Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 609-623
-
- Article
- Export citation
Range Spaces of Co-Analytic Toeplitz Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1261-1283
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
CLASSICAL PROPERTIES OF COMPOSITION OPERATORS ON HARDY–ORLICZ SPACES ON PLANAR DOMAINS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 256-271
-
- Article
-
- You have access
- Export citation