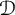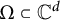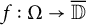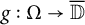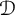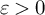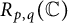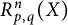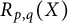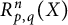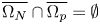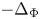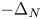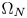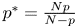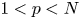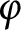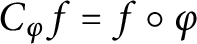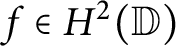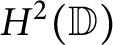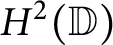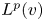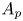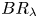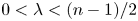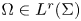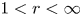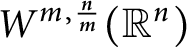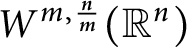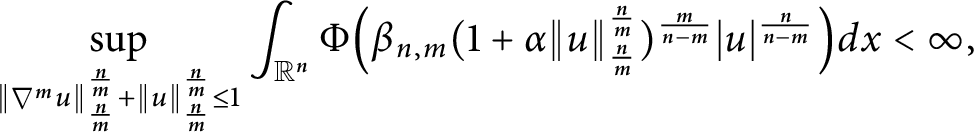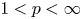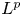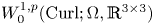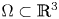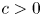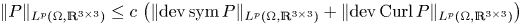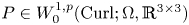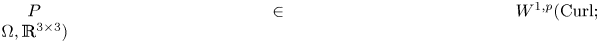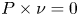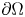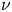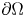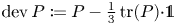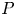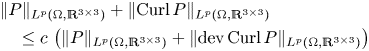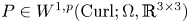Refine listing
Actions for selected content:
220 results in 46Exx
REFLEXIVITY INDEX OF THE PRODUCT OF SOME TOPOLOGICAL SPACES AND LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 376-387
- Print publication:
- April 2024
-
- Article
- Export citation
Determining sets for holomorphic functions on the symmetrized bidisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 984-996
- Print publication:
- September 2023
-
- Article
- Export citation
BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 737-752
- Print publication:
- March 2024
-
- Article
- Export citation
Estimates for generalized Bohr radii in one and higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 682-699
- Print publication:
- June 2023
-
- Article
- Export citation
Multiple solutions for a class of quasilinear problems with double criticality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 21 October 2022, pp. 1011-1047
-
- Article
- Export citation
Harnack inequality for the nonlocal equations with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1479-1502
- Print publication:
- October 2023
-
- Article
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
On Hardy kernels as reproducing kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 428-442
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractional interpolation inequality and radially symmetric ground states
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 937-957
- Print publication:
- June 2023
-
- Article
- Export citation
Non-Hilbertian tangents to Hilbertian spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 811-832
- Print publication:
- June 2023
-
- Article
- Export citation
Model spaces invariant under composition operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 204-217
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure data elliptic problems with generalized Orlicz growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 588-618
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted estimates for Bochner–Riesz operators on Lorentz spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 654-678
- Print publication:
- April 2023
-
- Article
- Export citation
Trudinger’s inequalities for Riesz potentials in Morrey spaces of double phase functionals on half spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 924-935
- Print publication:
- December 2022
-
- Article
- Export citation
A sharpened form of Adams-type inequalities on higher-order Sobolev spaces
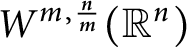 $W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach
$W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 895-905
- Print publication:
- December 2022
-
- Article
- Export citation
Partial regularity for minimizers of discontinuous quasiconvex integrals with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1191-1232
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extrapolation to weighted Morrey spaces with variable exponents and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 09 November 2021, pp. 1002-1027
-
- Article
- Export citation
Lp-trace-free generalized Korn inequalities for incompatible tensor fields in three space dimensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1477-1508
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FUNCTIONAL CALCULI FOR SECTORIAL OPERATORS AND RELATED FUNCTION THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 04 October 2021, pp. 1383-1463
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lorentz and Gale–Ryser theorems on general measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 857-878
- Print publication:
- August 2022
-
- Article
- Export citation